Problem #DES-180524

Problem

A set is a collection of objects of any specified kind, the objects are called elements or members, the objects in one set cannot repeat, namely $\{1,2,3\}$ and $\{1,2,2,2,3\}$ are identical sets. We denote a set by a capital letter $A$, or $B$ and write $x\in A$ if $x$ is an element of $A$, and $x\notin A$ if it is not. The notation $A=\{a,b,c,...\}$ means that the set $A$ consists of the elements $a,b,c,...$. The empty or void set, $\mathrm{\varnothing }$, has no elements. If all elements of $A$ are also in $B$, then we call $A$ a subset of $B$ and we write $A\subseteq B$. It is an axiom that the sets $A$ and $B$ are equal $A=B$ if they have the same elements. Namely, $A$ is a subset of $B$ and $B$ is a subset of $A$ at the same time.
For any sets $A$ and $B$, we define their union $A\cup B$, intersection $A\cap B$, and the difference $A-B$ as follows:

• the union $A\cup B$ is the set of all elements that belong to $A$ or $B$;

• the intersection $A\cap B$ is the set of elements that belong to both $A$ and $B$;

• the difference $A-B$ consists of those $x\in A$ that are do not belong to $B$.

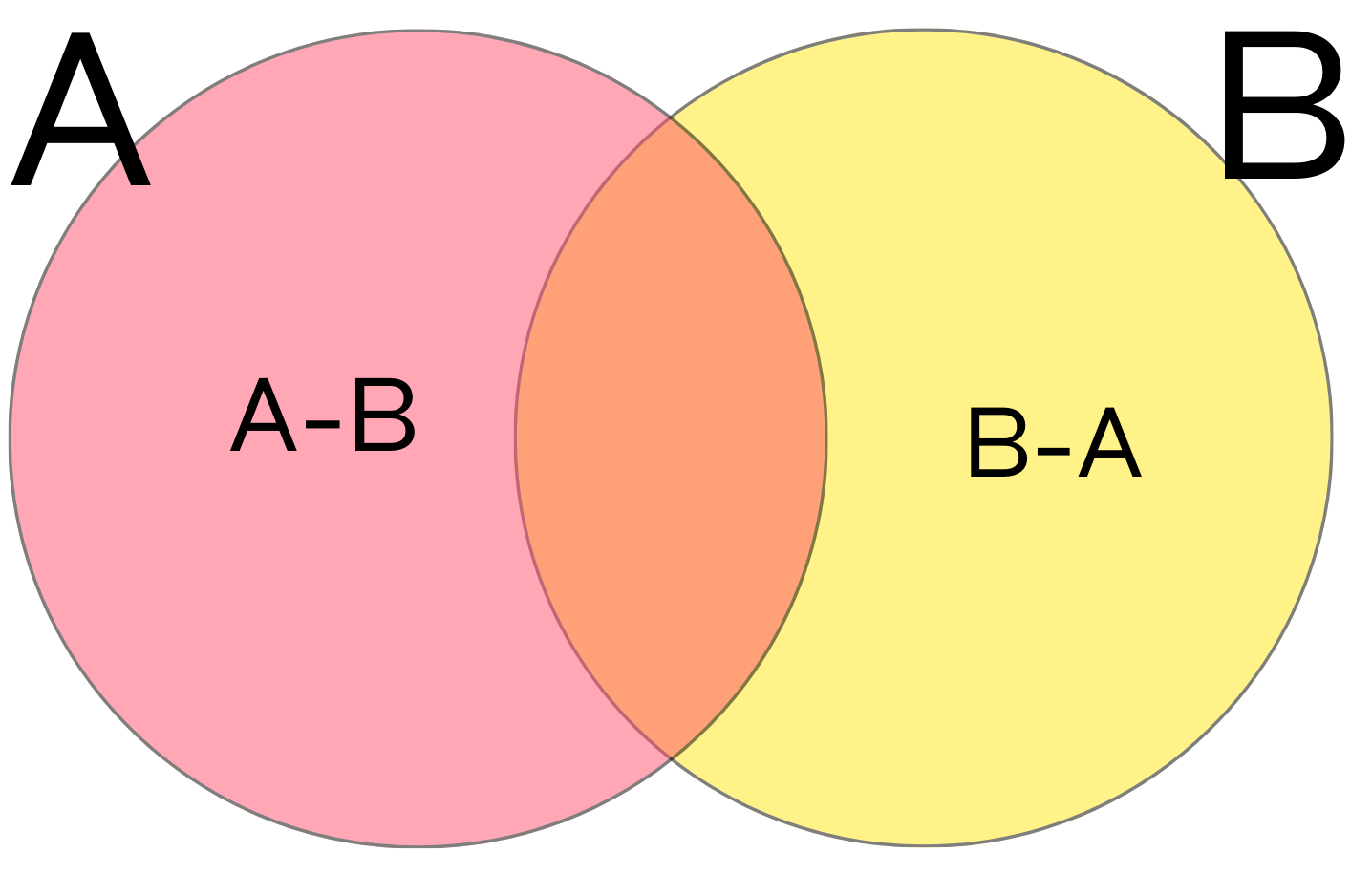
Sometimes it is useful to draw sets as Venn diagrams, on the diagram below the pink circle represents the set $A$, the yellow circle represents the set $B$, the orange part is the intersection $A\cap B$, the pink part is $A-B$, the yellow part is $B-A$, and the whole picture is the union $A\cup B$.