Problems

Two weighings. There are 7 coins which are identical on the surface, including 5 real ones (all of the same weight) and 2 counterfeit coins (both of the same weight, but lighter than the real ones). How can you find the 3 real coins with the help of two weighings on scales without weights?

Multiplication of numbers. Restore the following example of the multiplication of natural numbers if it is known that the sum of the digits of both factors is the same.

Restore the example of the multiplication.

Michael thinks of a number no less than \(1\) and no greater than \(1000\). Victoria is only allowed to ask questions to which Michael can answer “yes” or “no” (Michael always tells the truth). Can Victoria figure out which number Michael thought of by asking \(10\) questions?

There are 6 locked suitcases and 6 keys to them. At the same time, it is not known to which suitcase each key fits. What is the smallest number of attempts you need to make in order to open all the suitcases for sure? And how many attempts will it take there are not 6 but 10 keys and suitcases?

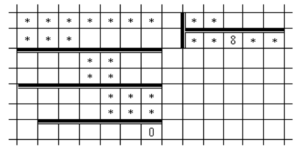
Decipher the following rebus (see the figure). Despite the fact that only two figures are known here, and all others are replaced by asterisks, the example can be restored.

Three people A, B, C counted a bunch of balls of four colors (see table).

Each of them correctly distinguished some two colors, and confused the numbers of the other two colours: one mixed up the red and orange, another – orange and yellow, and the third – yellow and green. The results of their calculations are given in the table.

How many balls of each colour actually were there?

A family went to the bridge at night. The dad can cross over it in 1 minute, the mom can cross it in 2, the child takes 5 minutes, and grandmother in 10 minutes. They have one flashlight. The bridge can only withstands two people at a time. How can they all cross the bridge in 17 minutes? (If two people pass, then they go at the lower of their speeds.) You can not move along a bridge without a flashlight. You can not shine it from a distance.

On the island of Contrast, both knights and liars live. Knights always tell the truth, liars always lie. Some residents said that the island has an even number of knights, and the rest said that the island has an odd number of liars. Can the number of inhabitants of the island be odd?

Jessica, Nicole and Alex received 6 coins between them: 3 gold coins and 3 silver coins. Each of them received 2 coins. Jessica doesn’t know which coins the others received but only which coins she has. Think of a question which Jessica can answer with either “yes”, “no” or “I don’t know” such that from the answer you can know which coins Jessica has.