Problems
Prove that for any positive integer \(n\) the inequality
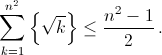
is true.
There is a group of 5 people: Alex, Beatrice, Victor, Gregory and Deborah. Each of them has one of the following codenames: V, W, X, Y, Z. We know that:
Alex is 1 year older than V,
Beatrice is 2 years older than W,
Victor is 3 years older than X,
Gregory is 4 years older than Y.
Who is older and by how much: Deborah or Z?
The order of books on a shelf is called wrong if no three adjacent books are arranged in order of height (either increasing or decreasing). How many wrong orders is it possible to construct from \(n\) books of different heights, if: a) \(n = 4\); b) \(n = 5\)?
What has a greater value: \(300!\) or \(100^{300}\)?
A traveller rents a room in an inn for a week and offers the innkeeper a chain of seven silver links as payment – one link per day, with the condition that they will be payed everyday. The innkeeper agrees, with the condition that the traveller can only cut one of the links. How did the traveller manage to pay the innkeeper?
There are 6 locked suitcases and 6 keys for them. It is not known which keys are for which suitcase. What is the smallest number of attempts do you need in order to open all the suitcases? How many attempts would you need if there are 10 suitcases and keys instead of 6?
Orcs and goblins, 40 creatures altogether, are standing in a rectangular formation of \(4\) rows and \(10\) columns. Is it possible that the total number of orcs in each row is \(7\), while the number of orcs in each column is the same?
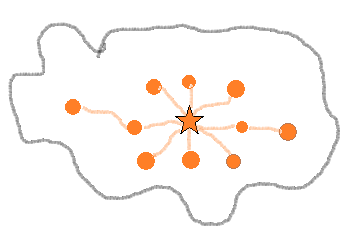
There are some cannons in every fortress on Cannon Island. The star marks the Grand Fortress, the capital, and the \(10\) circles mark \(10\) smaller fortresses. The total number of cannons located in all the fortresses along the east-west road is known to be \(130\). The total number of cannons along each of the other three roads is \(80\). Also it is known that there is a total of \(280\) cannons in all the fortresses. How many cannons are in the capital?
There are \(5\) directors of \(5\) banks sitting at the round table. Some of these banks have a negative balance (they owe more money than they have) and some have a positive balance (they have more money than they owe). It is known that for any 3 directors sitting next to each otehr, their 3 banks together have a positive balance. Does this mean that the \(5\) banks together have a positive balance?
A group of Martians and a group of Venusians got together for an important talk. At the start of the meeting, each Martian shook hands with 6 different Venusians, and each Venusian shook hands with 8 different Martians. It is known that 24 Martians took part in the meeting. How large was the delegation for Venus?