Problems
For each pair of real numbers \(a\) and \(b\), consider the sequence of numbers \(p_n = \lfloor 2 \{an + b\}\rfloor\). Any \(k\) consecutive terms of this sequence will be called a word. Is it true that any ordered set of zeros and ones of length \(k\) is a word of the sequence given by some \(a\) and \(b\) for \(k = 4\); when \(k = 5\)?
Note: \(\lfloor c\rfloor\) is the integer part, \(\{c\}\) is the fractional part of the number \(c\).
With a non-zero number, the following operations are allowed: \(x \rightarrow \frac{1+x}{x}\), \(x \rightarrow \frac{1-x}{x}\). Is it true that from every non-zero rational number one can obtain each rational number with the help of a finite number of such operations?
Calculate \(\int_0^{\pi/2} (\sin^2 (\sin x) + \cos^2 (\cos x))\,dx\).
Author: A.K. Tolpygo
An irrational number \(\alpha\), where \(0 <\alpha <\frac 12\), is given. It defines a new number \(\alpha_1\) as the smaller of the two numbers \(2\alpha\) and \(1 - 2\alpha\). For this number, \(\alpha_2\) is determined similarly, and so on.
a) Prove that for some \(n\) the inequality \(\alpha_n <3/16\) holds.
b) Can it be that \(\alpha_n> 7/40\) for all positive integers \(n\)?
What has a greater value: \(300!\) or \(100^{300}\)?
Prove that for every natural number \(n > 1\) the equality: \[\lfloor n^{1 / 2}\rfloor + \lfloor n^{1/ 3}\rfloor + \dots + \lfloor n^{1 / n}\rfloor = \lfloor \log_{2}n\rfloor + \lfloor \log_{3}n\rfloor + \dots + \lfloor \log_{n}n\rfloor\] is satisfied.
A numerical sequence is defined by the following conditions: \[a_1 = 1, \quad a_{n+1} = a_n + \lfloor \sqrt{a_n}\rfloor .\]
Prove that among the terms of this sequence there are an infinite number of complete squares.
Orcs and goblins, 40 creatures altogether, are standing in a rectangular formation of \(4\) rows and \(10\) columns. Is it possible that the total number of orcs in each row is \(7\), while the number of orcs in each column is the same?
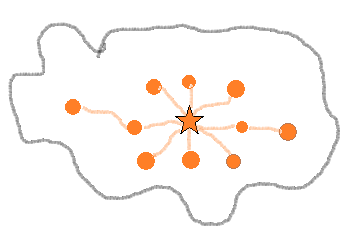
There are some cannons in every fortress on Cannon Island. The star marks the Grand Fortress, the capital, and the \(10\) circles mark \(10\) smaller fortresses. The total number of cannons located in all the fortresses along the east-west road is known to be \(130\). The total number of cannons along each of the other three roads is \(80\). Also it is known that there is a total of \(280\) cannons in all the fortresses. How many cannons are in the capital?
There are \(5\) directors of \(5\) banks sitting at the round table. Some of these banks have a negative balance (they owe more money than they have) and some have a positive balance (they have more money than they owe). It is known that for any 3 directors sitting next to each otehr, their 3 banks together have a positive balance. Does this mean that the \(5\) banks together have a positive balance?