Problems
Prove that for any positive integer \(n\) the inequality
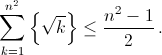
is true.
There is a group of 5 people: Alex, Beatrice, Victor, Gregory and Deborah. Each of them has one of the following codenames: V, W, X, Y, Z. We know that:
Alex is 1 year older than V,
Beatrice is 2 years older than W,
Victor is 3 years older than X,
Gregory is 4 years older than Y.
Who is older and by how much: Deborah or Z?
Prove that for every natural number \(n > 1\) the equality: \[\lfloor n^{1 / 2}\rfloor + \lfloor n^{1/ 3}\rfloor + \dots + \lfloor n^{1 / n}\rfloor = \lfloor \log_{2}n\rfloor + \lfloor \log_{3}n\rfloor + \dots + \lfloor \log_{n}n\rfloor\] is satisfied.
Orcs and goblins, 40 creatures altogether, are standing in a rectangular formation of \(4\) rows and \(10\) columns. Is it possible that the total number of orcs in each row is \(7\), while the number of orcs in each column is the same?
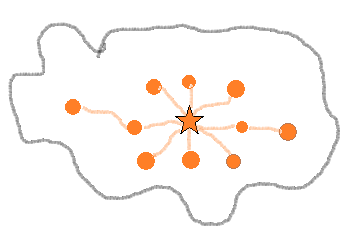
There are some cannons in every fortress on Cannon Island. The star marks the Grand Fortress, the capital, and the \(10\) circles mark \(10\) smaller fortresses. The total number of cannons located in all the fortresses along the east-west road is known to be \(130\). The total number of cannons along each of the other three roads is \(80\). Also it is known that there is a total of \(280\) cannons in all the fortresses. How many cannons are in the capital?
There are \(5\) directors of \(5\) banks sitting at the round table. Some of these banks have a negative balance (they owe more money than they have) and some have a positive balance (they have more money than they owe). It is known that for any 3 directors sitting next to each otehr, their 3 banks together have a positive balance. Does this mean that the \(5\) banks together have a positive balance?
A group of Martians and a group of Venusians got together for an important talk. At the start of the meeting, each Martian shook hands with 6 different Venusians, and each Venusian shook hands with 8 different Martians. It is known that 24 Martians took part in the meeting. How large was the delegation for Venus?
There are \(36\) warrior tomcats standing in a \(6 \times 6\) square formation. Each cat has several daggers strapped to his belt. Is it possible that the total number of daggers in each row is more than \(50\) and the total number of daggers in each column is less than \(50\)?
Francesca, Isabella and Lorenzo played chess together. Each child played \(10\) rounds.
Is it possible that Lorenzo played more rounds with Isabella than with Francesca?
A \(3 \times 3\) magic square is a square with different number from \(1\) to \(9\) in each of its \(9\) cells. The numbers in each row, column and diagonal sum up to \(15\). Show that there is a number \(5\) in the centre of the square.