Problems
Matt built a simple wooden hut to protect himself from the rain. From the side the hut looks like a right triangle with the right angle at the top. The longer part of the roof has 20 ft and the shorter one has 15 ft. What is the height of the hut in feet?
The three sides of a right triangle have all integer lengths. Show that at least one of them has an even length.
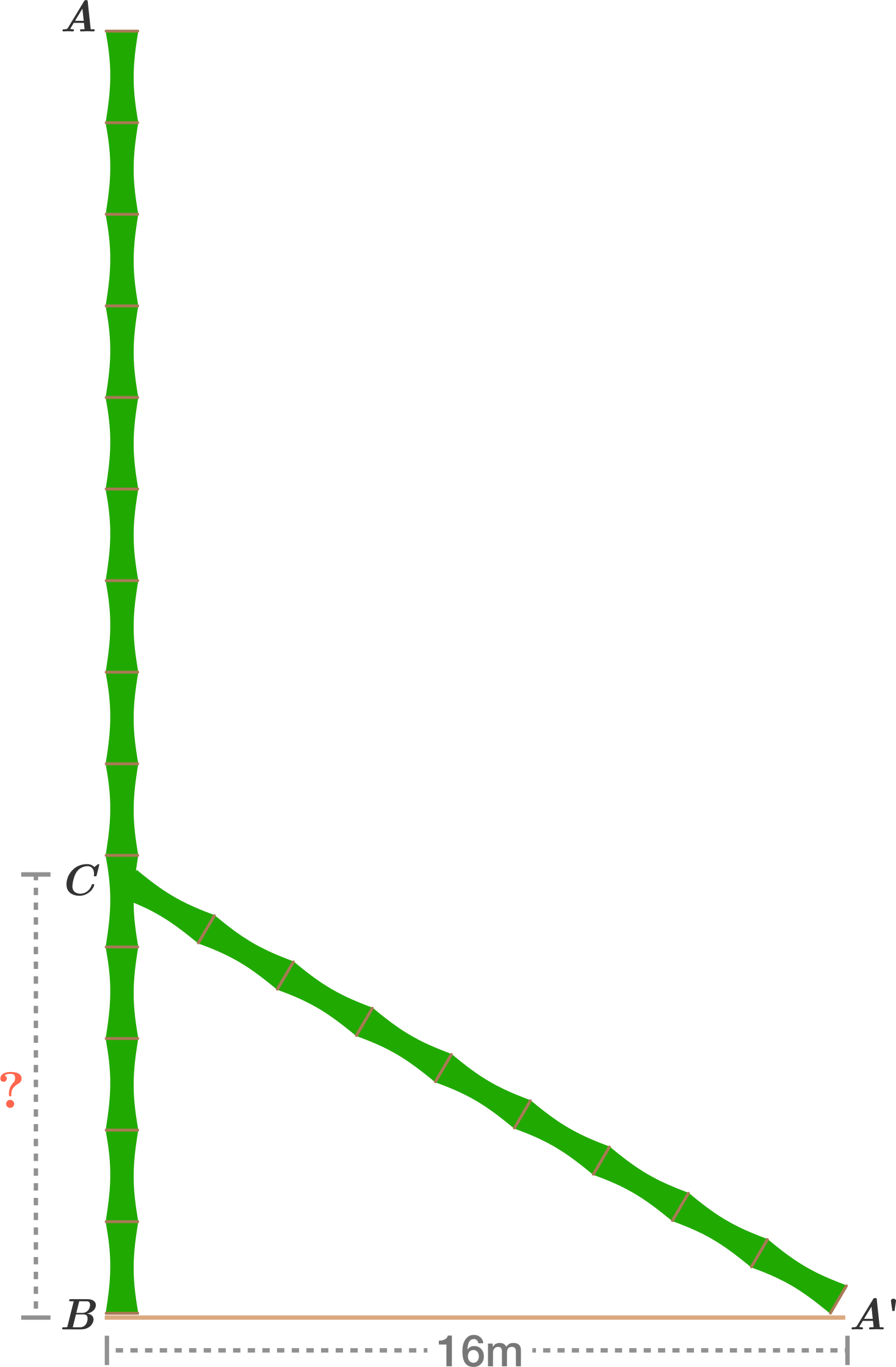
A bamboo tree, originally \(32\) metres high, broke in two parts. The end of the other one has fallen \(16\) metres away from the trunk. How high is the remaining vertical part of the bamboo tree?
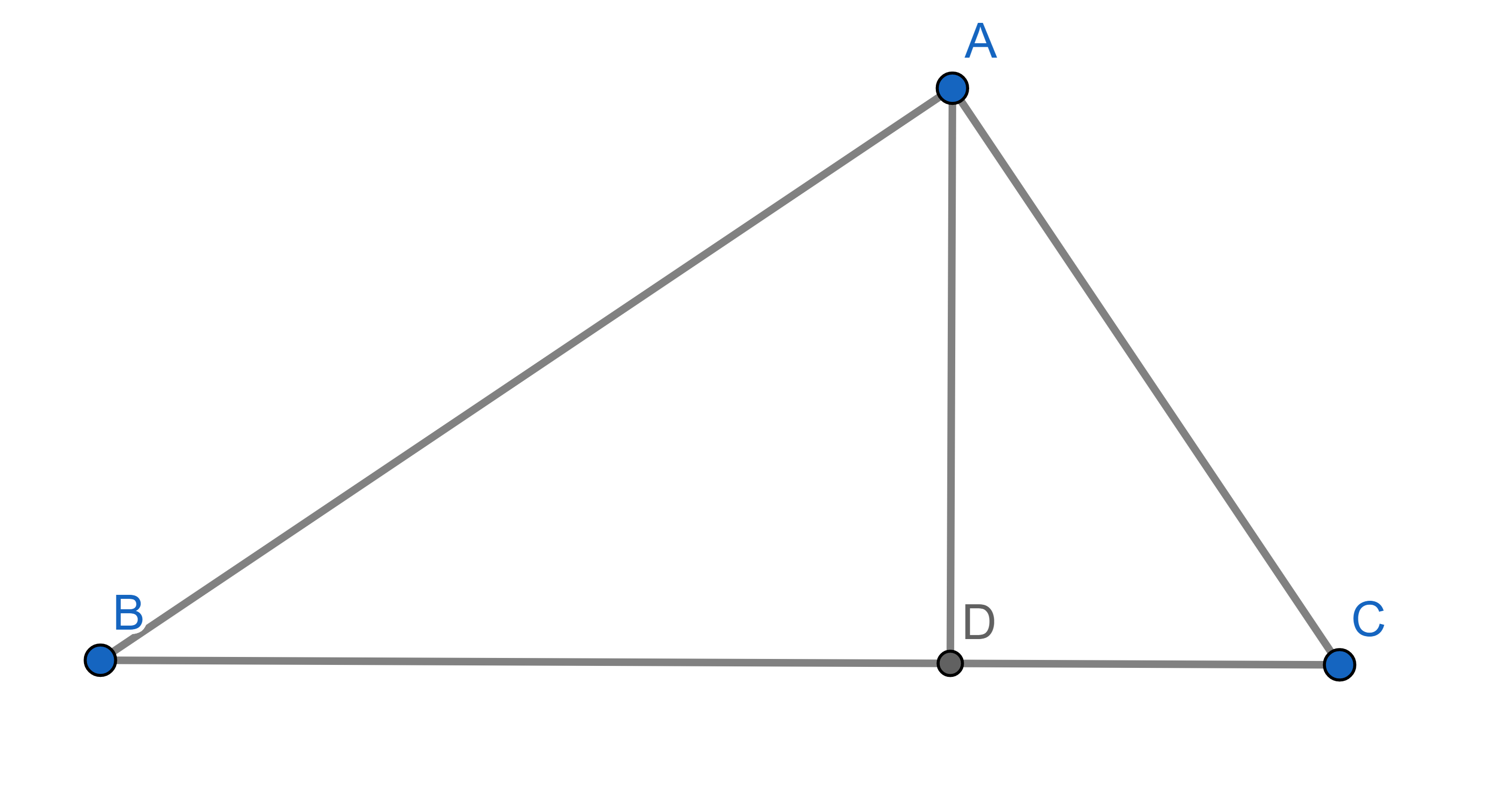
Matt has built an additional support for his hut (\(AD\)), whose length is \(12\)ft, and the base \(BC\) is \(25\)ft. We also know \(AB = 20\) and \(AC = 15\). What are the distances \(|BD|\) and \(|DC|\)? Show that \(|AD|^2=|BD| \times |AC|\) in this particular case. Do you think it is true in general?
Can you build a right-angled triangle using 25 identical matches without breaking them? You have to use them all. If yes, show how. If not, show why.
On the sides of a right-angled triangle three equilateral triangles were built. Show that the areas of two of the two smaller ones sum up to the area of the larger one.
One triangle has sidelengths \(25,25\) and \(48\), and another triangle has sidelengths \(25,25\) and \(14\). Which of them has a larger area?
The marked pink segment (tangent to the inner circle) has length \(1\). Find the area of the green annulus.

A triple of natural numbers \(a,b,c\) such that \(a^2 + b^2 = c^2\) is called a Pythagorean triple. There are some small Pythagorean triples that are well-known, like \(3,4,5\) and \(5,12,13\). Let us have a look at the latter one. We can notice an interesting thing: not only \(5^2+12^2=13^2\), but also \(5^2 = 25 = 12+13\) and \(13-12=1\). Use that as an inspiration to find an idea of how to generate some more Pythagorean triples. Check if they are correct by plugging them into the equation \(a^2 +b^2 = c^2\).
Two semicircles and one circle were drawn on the sides of a right triangle. The circle whose centre is in the midpoint of the hypothenuse actually goes through the right angle corner – this is a general fact, but you don’t need to prove it here. If the two shorter sides of the triangle are \(3\) and \(4\), what is the total area of the red region?