Problems
A cherry which is a ball of radius r is dropped into a round glass whose axial section is the graph of the function \(y = x^4\). At what maximum r will the ball touch the most bottom point of the bottom of the glass? (In other words, what is the maximum radius r of a circle lying in the region \(y \geq x^4\) and containing the origin?).
Consider the powers of the number five: 1, 5, 25, 125, 625, ... We form the sequence of their first digits: 1, 5, 2, 1, 6, ...
Prove that any part of this sequence, written in reverse order, will occur in the sequence of the first digits of the powers of the number two (1, 2, 4, 8, 1, 3, 6, 1, ...).
Three functions are written on the board: \(f_1 (x) = x + 1/x\), \(f_2 (x) = x^2, f_3 (x) = (x - 1)^2\). You can add, subtract and multiply these functions (and you can square, cube, etc. them). You can also multiply them by an arbitrary number, add an arbitrary number to them, and also do these operations with the resulting expressions. Therefore, try to get the function \(1/x\).
Prove that if you erase any of the functions \(f_1, f_2, f_3\) from the board, it is impossible to get \(1/x\).
A continuous function \(f\) has the following properties:
1. \(f\) is defined on the entire number line;
2. \(f\) at each point has a derivative (and thus the graph of f at each point has a unique tangent);
3. the graph of the function \(f\) does not contain points for which one of the coordinates is rational and the other is irrational.
Does it follow that the graph of \(f\) is a straight line?
For each pair of real numbers \(a\) and \(b\), consider the sequence of numbers \(p_n = \lfloor 2 \{an + b\}\rfloor\). Any \(k\) consecutive terms of this sequence will be called a word. Is it true that any ordered set of zeros and ones of length \(k\) is a word of the sequence given by some \(a\) and \(b\) for \(k = 4\); when \(k = 5\)?
Note: \(\lfloor c\rfloor\) is the integer part, \(\{c\}\) is the fractional part of the number \(c\).
Solve the equation: \((x^3 - 2) (2^{\sin x} - 1) + (2^{x^3} - 4) \sin x = 0\).
Seven triangular pyramids stand on the table. For any three of them, there is a horizontal plane that intersects them along triangles of equal area. Prove that there is a plane intersecting all seven pyramids along triangles of equal area.
Prove that for all \(x\), \(0 < x < \pi /3\), we have the inequality \(\sin 2x + \cos x > 1\).
Prove that for any positive integer \(n\) the inequality
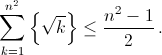
is true.
Find the sum \(1/3 + 2/3 + 2^2/3 + 2^3/3 + \dots + 2^{1000}/3\).