Problems

Prove that for any positive integer \(n\) the inequality

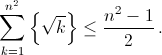
is true.

The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function

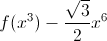
also increases for all positive \(x\).

Prove that if the numbers \(x, y, z\) satisfy the following system of equations for some values of \(p\) and \(q\): \[\begin{aligned} y &= x^2 + px + q,\\ z &= y^2 + py + q,\\ x &= z^2 + pz + q, \end{aligned}\] then the inequality \(x^2y + y^2z + z^2x \geq x^2z + y^2x + z^2y\) is satisfied.

Let \(p\) and \(q\) be positive numbers where \(1 / p + 1 / q = 1\). Prove that \[a_1b_1 + a_2b_2 + \dots + a_nb_n \leq (a_1^p + \dots a_n^p)^{1/p}(b_1^q +\dots + b_n^q)^{1/q}\] The values of the variables are considered positive.

Solve the inequality: \(\lfloor x\rfloor \times \{x\} < x - 1\).