Problems

At a contest named “Ah well, monsters!”, 15 dragons stand in a row. Between neighbouring dragons the number of heads differs by 1. If the dragon has more heads than both of his two neighbors, he is considered cunning, if he has less than both of his neighbors – strong, the rest (including those standing at the edges) are considered ordinary. In the row there are exactly four cunning dragons – with 4, 6, 7 and 7 heads and exactly three strong ones – with 3, 3 and 6 heads. The first and last dragons have the same number of heads.

a) Give an example of how this could occur.

b) Prove that the number of heads of the first dragon in all potential examples is the same.

Decipher the following puzzle. All the numbers indicated by the letter E, are even (not necessarily equal); all the numbers indicated by the letter O are odd (also not necessarily equal).

In a certain kingdom there were 32 knights. Some of them were vassals of others (a vassal can have only one suzerain, and the suzerain is always richer than his vassal). A knight with at least four vassals is given the title of Baron. What is the largest number of barons that can exist under these conditions?

(In the kingdom the following law is enacted: “the vassal of my vassal is not my vassal”).

Find the largest number of colours in which you can paint the edges of a cube (each edge with one colour) so that for each pair of colours there are two adjacent edges coloured in these colours. Edges are considered to be adjacent if they have a common vertex.

There are 40 identical cords. If you set any cord on fire on one side, it burns, and if you set it alight on the other side, it will not burn. Ahmed arranges the cords in the form of a square (see the figure below, each cord makes up a side of a cell). Then, Helen arranges 12 fuses. Will Ahmed be able to lay out the cords in such a way that Helen will not be able to burn all of them?

In each cell of a board of size \(5\times5\) a cross or a nought is placed, and no three crosses are positioned in a row, either horizontally, vertically or diagonally. What is the largest number of crosses on the board?

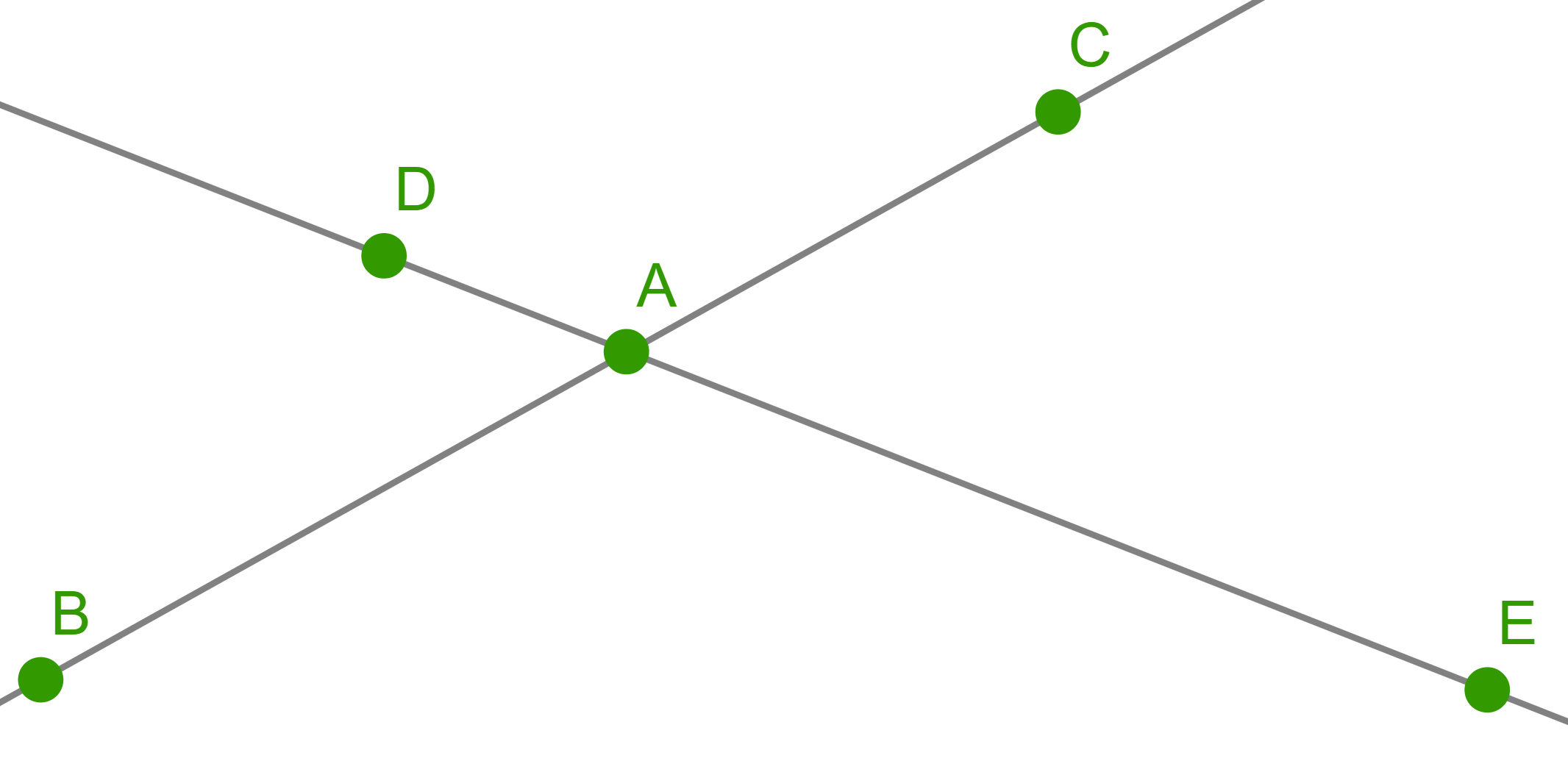
Five oaks are planted along two linear park alleys in such a way that there are three oaks along each alley, see picture. Where should we plant the sixth oak so that it will be possible to lay two more linear alleys, along each of which there would also be three oak trees growing?

The smell of a flowering lavender plant diffuses through a radius of 20 m around it. How many lavender plants must be planted along a straight 400m path so that the smell of the lavender reaches every point on the path.

Elephants, rhinoceroses, giraffes. In all zoos where there are elephants and rhinoceroses, there are no giraffes. In all zoos where there are rhinoceroses and there are no giraffes, there are elephants. Finally, in all zoos where there are elephants and giraffes, there are also rhinoceroses. Could there be a zoo in which there are elephants, but there are no giraffes and no rhinoceroses?

Among 4 people there are no three with the same name, the same middle name and the same surname, but any two people have either the same first name, middle name or surname. Can this be so?