Problems
The order of books on a shelf is called wrong if no three adjacent books are arranged in order of height (either increasing or decreasing). How many wrong orders is it possible to construct from \(n\) books of different heights, if: a) \(n = 4\); b) \(n = 5\)?
What has a greater value: \(300!\) or \(100^{300}\)?
A numerical sequence is defined by the following conditions: \[a_1 = 1, \quad a_{n+1} = a_n + \lfloor \sqrt{a_n}\rfloor .\]
Prove that among the terms of this sequence there are an infinite number of complete squares.
Prove that the 13th day of the month is more likely to occur on a Friday than on other days of the week. It is assumed that we live in the Gregorian style calendar.
In the first term of the year Daniel received five grades in mathematics with each of them being on a scale of 1 to 5, and the most common grade among them was a 5 . In this case it turned out that the median of all his grades was 4, and the arithmetic mean was 3.8. What grades could Daniel have?
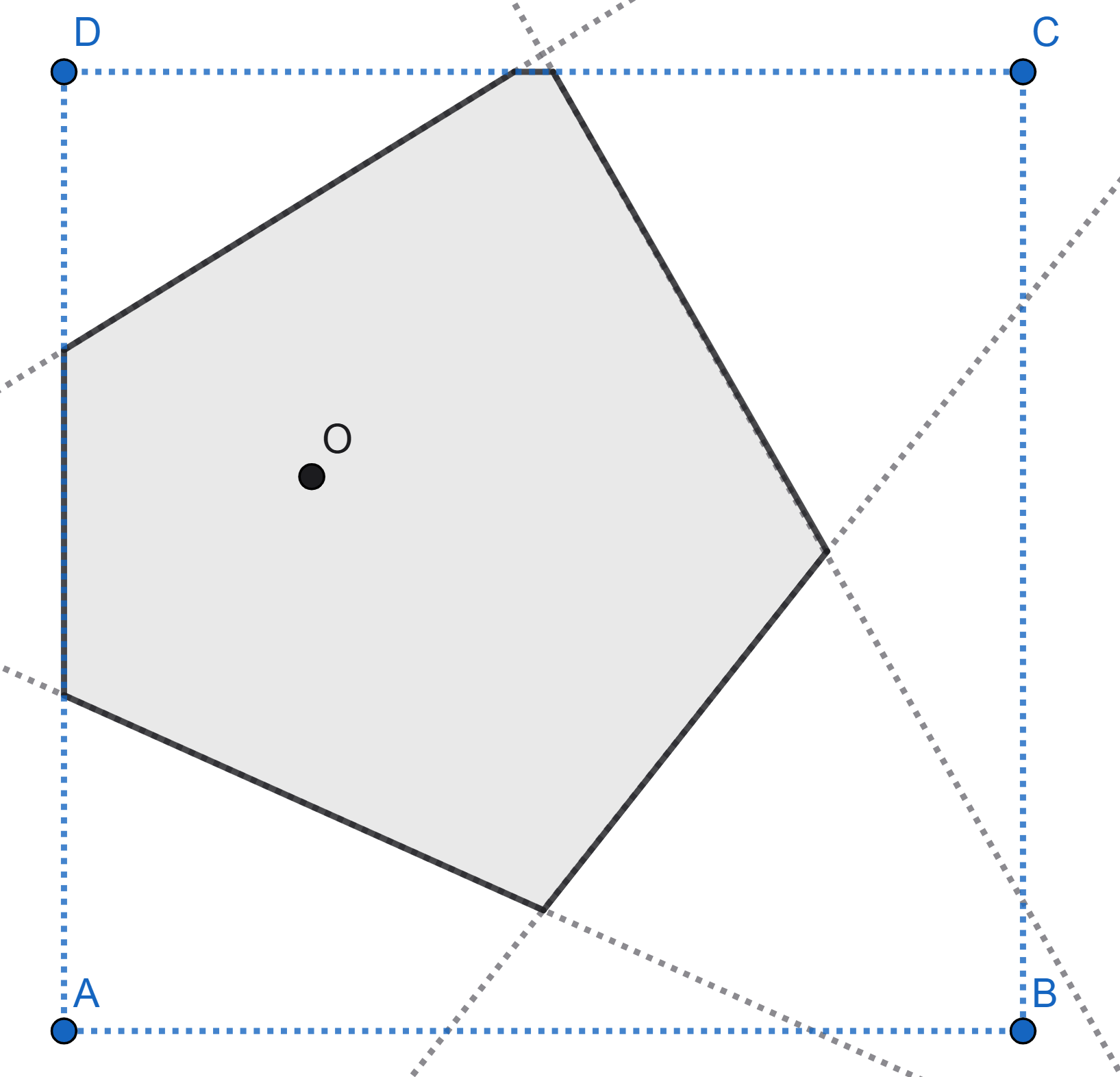
The point \(O\) is randomly chosen on piece of square paper. Then the square is folded in such a way that each vertex is overlaid on the point \(O\). The figure shows one of the possible folding schemes. Find the mathematical expectation of the number of sides of the polygon that appears.
Is it possible to place the numbers \(1, 2,\dots 12\) around a circle so that the difference between any two adjacent numbers is 3, 4, or 5?
In March 2015 a teacher ran 11 sessions of a maths club. Prove that if no sessions were run on Saturdays or Sundays there must have been three days in a row where a session of the club did not take place. The 1st March 2015 was a Sunday.
In any group of 10 children, out of a total of 60 pupils, there will be three who are in the same class. Will it always be the case that amongst the 60 pupils there will be: 1) 15 classmates? 2) 16 classmates?
We are given a table of size \(n \times n\). \(n-1\) of the cells in the table contain the number \(1\). The remainder contain the number \(0\). We are allowed to carry out the following operation on the table:
1. Pick a cell.
2. Subtract 1 from the number in that cell.
3. Add 1 to every other cell in the same row or column as the chosen cell.
Is it possible, using only this operation, to create a table in which all the cells contain the same number?