Problems
Find all functions \(f (x)\) such that \(f (2x + 1) = 4x^2 + 14x + 7\).
The function \(f (x)\) is defined and satisfies the relationship \((x-1) f((x=1)/(x-1)) - f (x) = x\) for all \(x \neq 1\). Find all such functions.
Find all the functions \(f\colon \mathbb {R} \rightarrow \mathbb {R}\) which satisfy the inequality \(f (x + y) + f (y + z) + f (z + x) \geq 3f (x + 2y + 3z)\) for all \(x, y, z\).
Is there a bounded function \(f\colon \mathbb{R} \rightarrow \mathbb{R}\) such that \(f (1)> 0\) and \(f (x)\) satisfies the inequality \(f^2 (x + y) \geq f^2 (x) + 2f (xy) + f^2 (y)\) for all \(x, y \in \mathbb{R}\)?
The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function
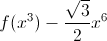
also increases for all positive \(x\).
On a function \(f (x)\), defined on the entire real line, it is known that for any \(a>1\) the function \(f (x) + f (ax)\) is continuous on the whole line. Prove that \(f (x)\) is also continuous on the whole line.
A convex figure and point \(A\) inside it are given. Prove that there is a chord (that is, a segment joining two boundary points of a convex figure) passing through point \(A\) and dividing it in half at point \(A\).
Suppose that there are 15 prime numbers forming an arithmetic progression with a difference of \(d\). Prove that \(d >30,000\).
Prove that the function \(\cos \sqrt {x}\) is not periodic.
Find the largest value of the expression \(a + b + c + d - ab - bc - cd - da\), if each of the numbers \(a\), \(b\), \(c\) and \(d\) belongs to the interval \([0, 1]\).