Problems

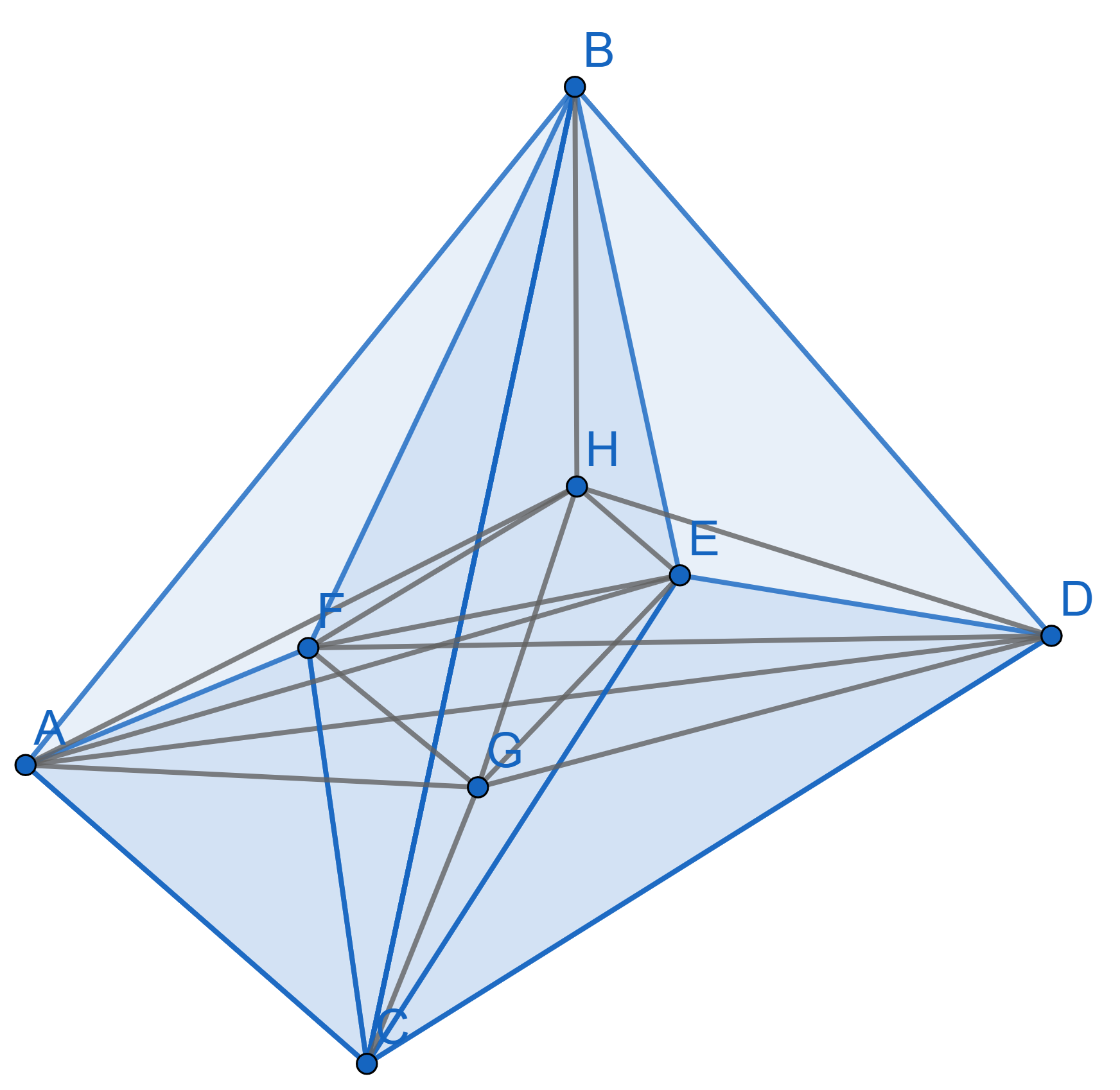
Draw a Sperner’s coloring for the following \(3\)-dimensional simplex. The blue segments are visible, the grey ones are inside the tetrahedron. The point \(F\) is on the face \(ABC\), point \(E\) is on the face \(BCD\), point \(G\) is on the face \(ACD\) and the point \(H\) is on the face \(ABD\).

Prove Sperner’s lemma in dimension \(1\), namely on a line.
The simplex in this case is just a segment, the triangulation is subdivision of the segment into multiple small segments, and the conditions of a Sperner’s coloring are the following:

• There are only two colors;

• The opposite ends of the main segment are colored differently;

Then one needs to prove that there exists a small segment with two ends colored in different colors. In particular there is an odd number of such small segments.

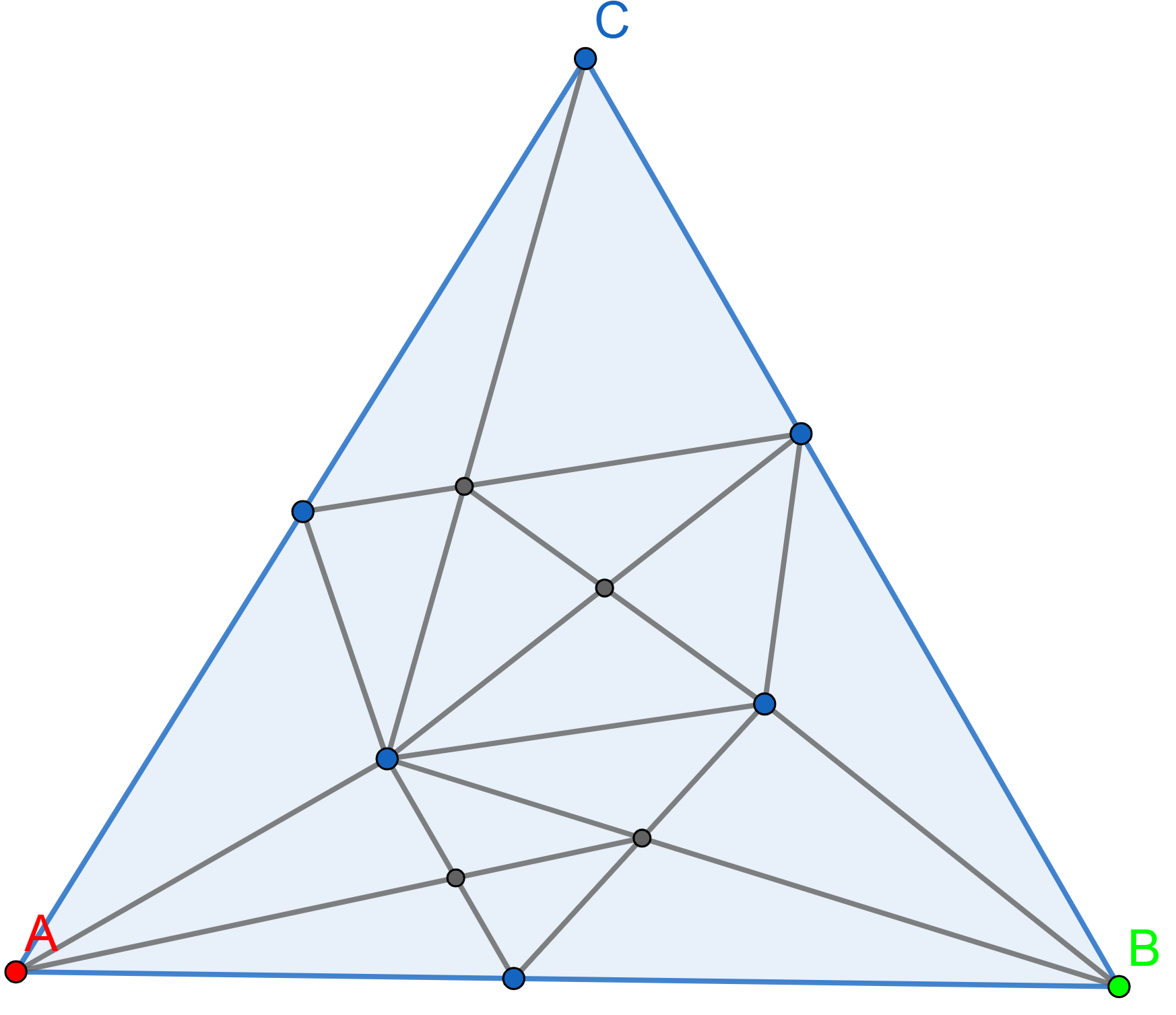
Draw Sperner’s coloring for the following triangulation. Try to avoid rainbow triangles at all costs.

Seven Smurfs live in seven mushroom houses. There is a tunnel between every pair of houses, so from any house you can walk to any other house. One of the Smurfs, Clumsy, starts walking from his house, but he must not use the same tunnel more than once. He keeps walking until he reaches a house where all the tunnels have already been used. Where will Clumsy’s journey end?