We solve problems

Problem #PRU-97956

Problems Geometry Plane geometry Polygons Regular polygons Discrete Mathematics Algorithm Theory Game theory Symmetric strategies

12–14 2.0

a) The vertices (corners) in a regular polygon with 10 sides are colored black and white in an alternating fashion (i.e. one vertex is black, the next is white, etc). Two people play the following game. Each player in turn draws a line connecting two vertices of the same color. These lines must not have common vertices (i.e. must not begin or end on the same dot as another line) with the lines already drawn. The winner of the game is the player who made the final move. Which player, the first or the second, would win if the right strategy is used?

b) The same problem, but for a regular polygon with 12 sides.

Problem #PRU-100430

Problems Geometry Solid geometry Parallelepipeds Special cases of parallelepipeds Cube Discrete Mathematics Set theory and logic Logic and set theory

The edges of a cube are assigned with integer values. For each vertex we look at the numbers corresponding to the three edges coming from this vertex and add them up. In case we get 8 equal results we call such cube “cute”. Are there any “cute” cubes with the following numbers corresponding to the edges:

(a) \(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\);

(b) \(-6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, 6\)?

Problem #PRU-100454

Problems Discrete Mathematics Set theory and logic Mathematical logic Paradoxes Geometry Plane geometry Quadrilateral Parallelogram Special cases Rectangles and squares. Criteria and properties

The area of a rectangle is 1 cm\(^2\). Can its perimeter be greater than 1 km?

Problem #PRU-58082

Problems Geometry Plane geometry Geometrical inequalities Inequalities in a triangle A segment inside the triangle is smaller than the largest side ,Problems Geometry Plane geometry Triangles Types of triangles Right-angled triangles Pythagorean theorem and its converse

12–14 4.0

A \(3\times 4\) rectangle contains 6 points. Prove that amongst them there will be two points, such that the distance between them is no greater than \(\sqrt5\).

Problem #PRU-58089

Problems Geometry Plane geometry Convex and non-convex figures Convex polygons Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–15 4.0

What is the minimum number of points necessary to mark inside a convex \(n\)-gon, so that at least one marked point always lies inside any triangle whose vertices are the vertices of the polygon?

Problem #PRU-73727

Problems Number Theory Divisibility Divisibility of a number. General properties Geometry Solid geometry Lines and planes in space Methods Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Out of the given numbers 1, 2, 3, ..., 1000, find the largest number \(m\) that has this property: no matter which \(m\) of these numbers you delete, among the remaining \(1000 - m\) numbers there are two, of which one is divisible by the other.

Problem #PRU-7646

Problems Geometry Plane geometry Area Triangle area

10–12 3.0

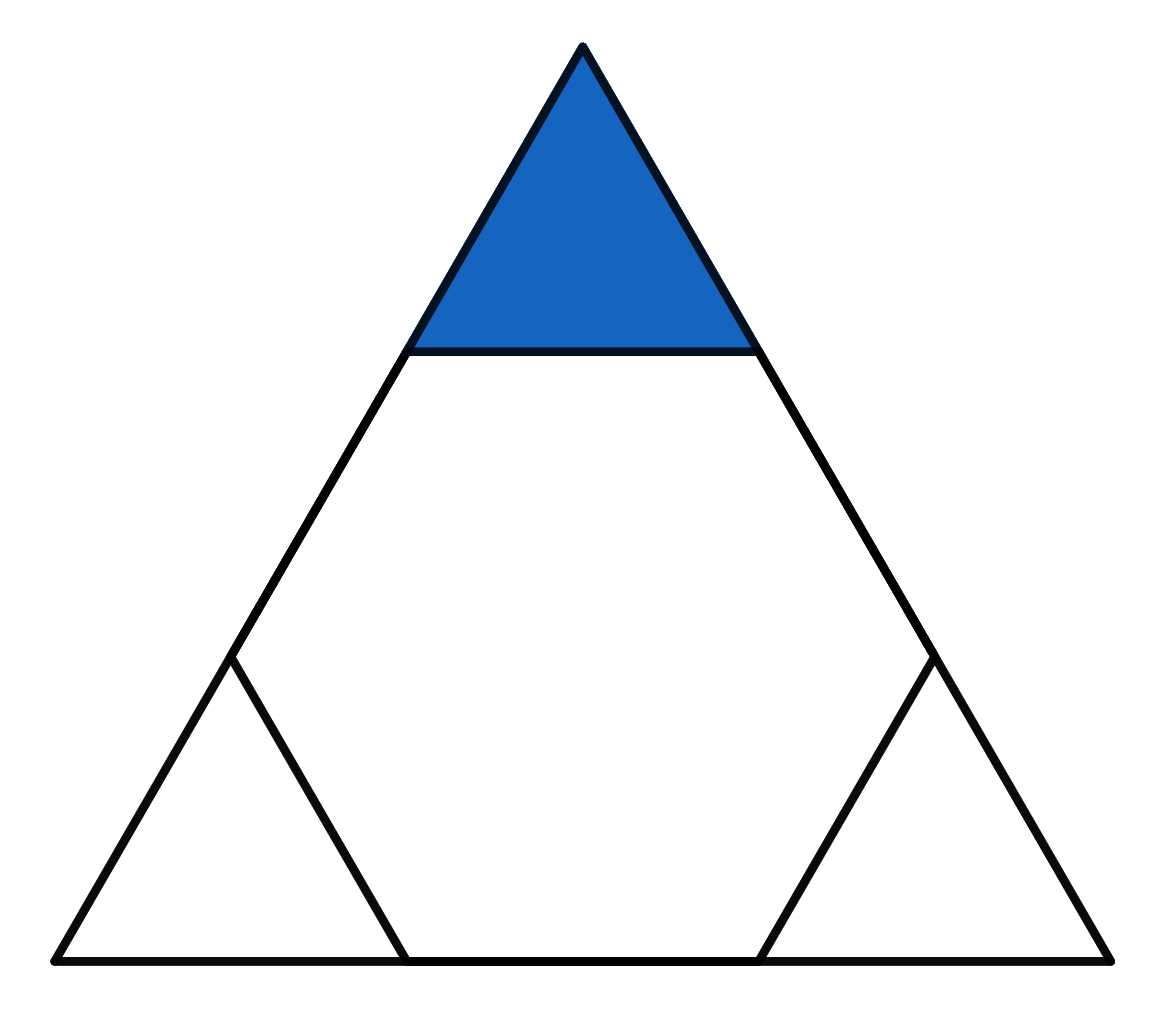
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.

Problem #PRU-7650

Problems Geometry Plane geometry Area Area of a circle, sector, segment

11–13 3.0

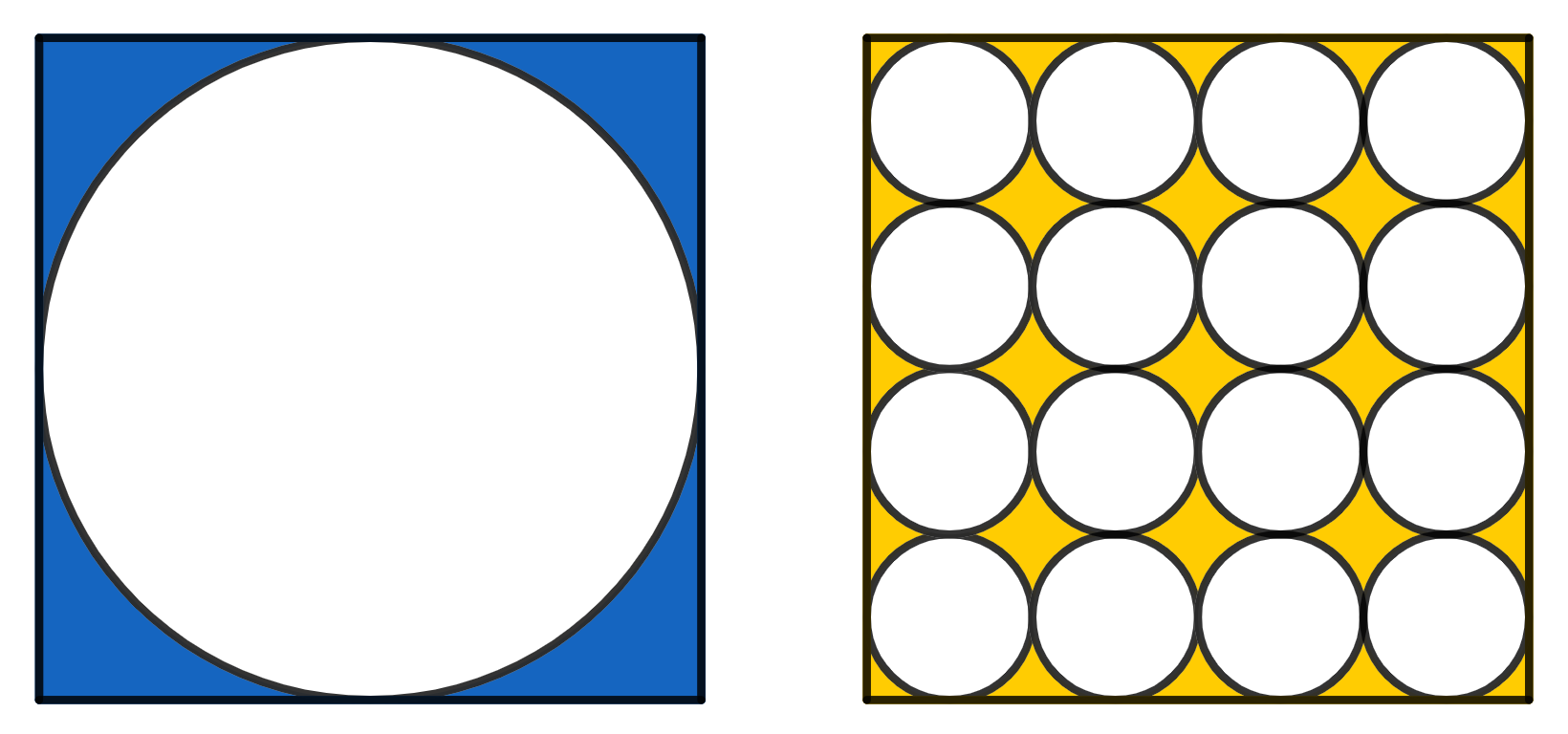
On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?

Problem #PRU-7653

Problems Geometry Plane geometry Area Area ratio Finding the area by rearrangment

12–14 4.0

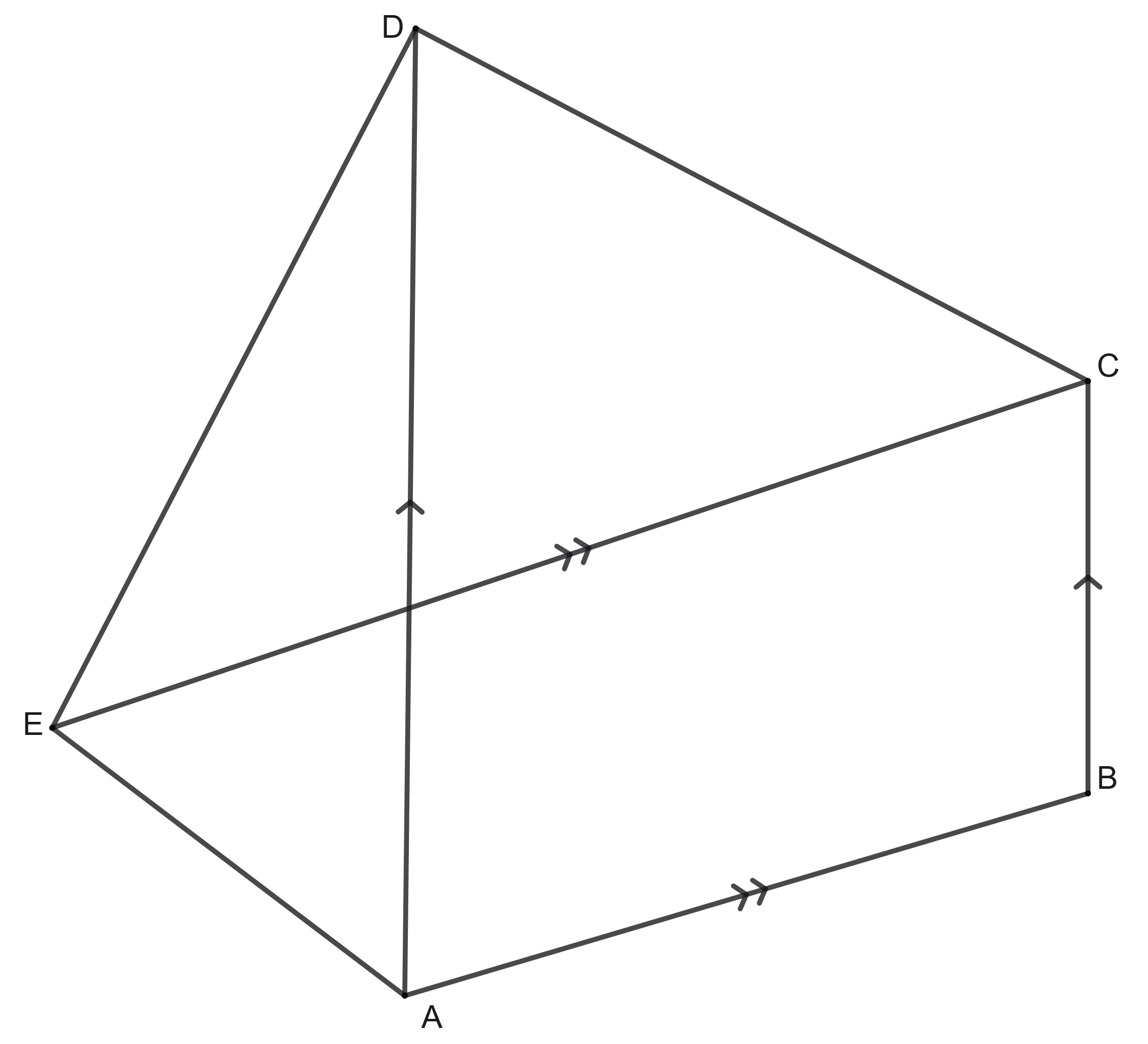
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.

Problem #PRU-79426

Problems Geometry Plane geometry Triangles Types of triangles Equilateral triangle Discrete Mathematics Combinatorics Painting problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–14 3.0

A white plane is arbitrarily sprinkled with black ink. Prove that for any positive \(l\) there exists a line segment of length \(l\) with both ends of the same colour.