Problems
Many maths problems begin with the question “Is it possible…?”. In these kinds of problems, what you need to do depends on what you think is true.
If you believe it is possible, then you must give an example that really satisfies the conditions in the problem.
If you believe it is not possible, then you must explain clearly why it cannot be done.
When trying to build an example, it often helps to ask yourself extra questions to narrow things down: “How could it be possible?”, or “What properties must a correct example have?”.
On the other hand, if you have been trying to build an example for a while and nothing works, perhaps the answer is that it is impossible. In that case, look for a property that any example would need to have — and then show why that property cannot actually happen. Let’s see some examples!
Welcome back! We hope you all had a great summer and now you are ready for the new school year full of fun problems in mathematics. We decided to start with warm-up topic called dissections, so today we will cut various shapes into more elaborate geometric figures in order to reassemble them into a different shape.
Today we will practice to encrypt and decipher information using some
of the most common codes. Majority of the codes in use can be alphabetic
and numeric, namely one may want to encode a word, a phrase, or a
number, or just any string of symbols using either letters, or numbers,
or both. Some of the codes, however may use various other symbols to
encrypt the information. To solve some of the problems you will need the
correspondence between alphabet letters and numbers
0.85
@*26c@ A & B & C &
D &E & F &G &H &I &J &K &L
&M&N&O&P&Q&R&S&T&U&V&W&X&Y&Z
1 & 2 &
3&4&5&6&7&8&9&10&11&12&13&14&15&16&17&18&19&20&21&22&23&24&25&26
Long ago in a galaxy far away there was a planet of liars and truth
tellers, it is known that liars always tell lie, and truth tellers
always respond with correct statements. All the inhabitants of the
planet look identical to each other, so there is no way to distinguish
between liars and truth tellers just by looking at them.
The planet is ruled by the government, where one may encounter honest
governors as well as liars. The government is controlled by the High
Council, where again one can meet liars and truth tellers.
Last weekend we held the verbal challenge and today we decided to demonstrate solutions of the most juicy problems.
Today we will focus on the study of Euclidean geometry of plane figures. Around 300 BCE a Greek mathematician Euclid developed a rigorous way to study plane geometry in his work Elements based on axioms (statement assumed to be correct) and theorems (statements deduced from axioms). The axioms of Euclidean Elements are the following:
For any two different points, there exists a line containing these two points, and this line is unique.
A straight line segment can be prolonged indefinitely.
A circle is defined by a point for its centre and a distance for its radius.
All right angles are equal.
For any line \(L\) and point \(P\) not on \(L\), there exists a line through \(P\) not meeting \(L\), and this line is unique.
In examples we deduce from the axioms above the following basic
principles:
1. The supplementary angles (angles "hugging" a straight line) add up to
\(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
3. A line cutting two parallel lines cuts them at the same angles (these
are called corresponding angles).
4. In an isosceles triangle (which has two sides of equal lengths), the
two angles touching the third side are equal.
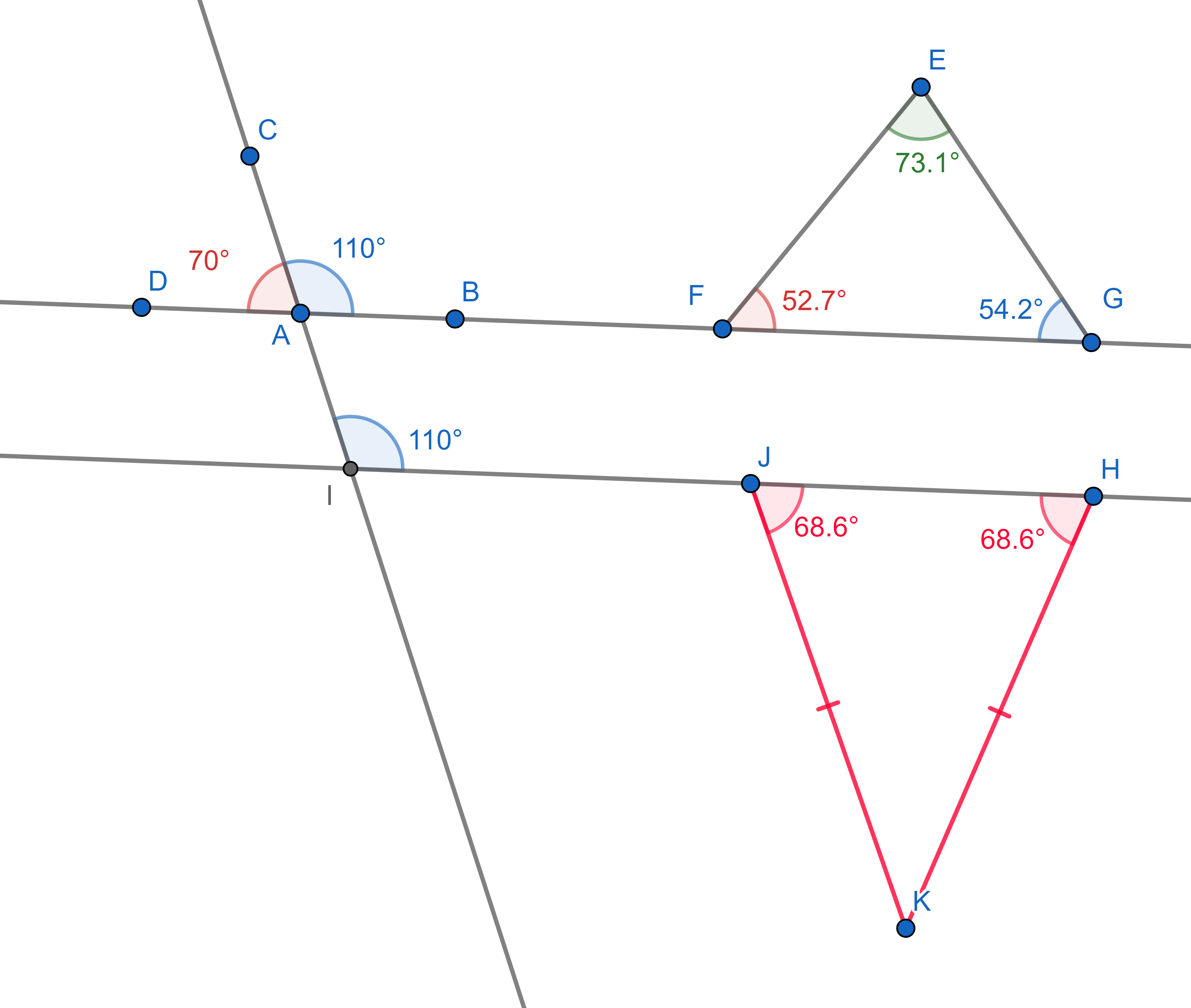
Let’s have a look at some examples of how to apply these axioms to prove geometric statements.
Sometimes different areas in mathematics are more related than they seem to be. A lot of algebraic expressions have geometric interpretation, and a lot of them can be used to solve problems in number theory.
Today we will solve several logic problems that revolve about a very
simple idea. Imagine you are in a room in a dungeon and you can see
doors leading out of the room. Some of them lead to the treasure and
some of them lead to traps. It is possible that all doors lead to
treasure or all lead to traps, but it is also possible that one door
leads to treasure and all other lead to traps. Unless specified, there
is always something behind the door.
Each door has a sign with a statement on it, but those statements are
not always true. You have a dungeon guide, who is always honest with you
and will tell you something about the truthfulness of the statements on
the doors, but it will be up to you to put it all together and pick the
correct door... or walk away, if you believe there is no treasure.
Generally, when a line intersects a circle, it creates two different
points of intersection. However, sometimes there is only one point. In
such case we say the line is tangent to the circle. For
example on the picture below the line \(CD\) intersects the circle at two points
\(D\) and \(E\) and the line \(CB\) is tangent to the circle. To solve the
problems today we will need the following theorem.
Theorem: The radius \(AB\) is perpendicular to the tangent line
\(BC\).
Sometimes one can guess certain multiples of a number just by looking at it, the idea of this sheet is to learn to recognise quickly using tricks when a natural number is divisible by another number.