Problems

There are 6 locked suitcases and 6 keys for them. It is not known which keys are for which suitcase. What is the smallest number of attempts do you need in order to open all the suitcases? How many attempts would you need if there are 10 suitcases and keys instead of 6?

Decipher the following puzzle. All the numbers indicated by the letter E, are even (not necessarily equal); all the numbers indicated by the letter O are odd (also not necessarily equal).

In a vase, there is a bouquet of 7 white and blue lilac branches. It is known that 1) at least one branch is white, 2) out of any two branches, at least one is blue. How many white branches and how many blue are there in the bouquet?

In a certain kingdom there were 32 knights. Some of them were vassals of others (a vassal can have only one suzerain, and the suzerain is always richer than his vassal). A knight with at least four vassals is given the title of Baron. What is the largest number of barons that can exist under these conditions?

(In the kingdom the following law is enacted: “the vassal of my vassal is not my vassal”).

Numbers \(1,2,\dots,20\) are written on a whiteboard. In one go Louise is allowed to wipe out any two numbers \(a\) and \(b\), and write their sum \(a+b\) instead. Louise enjoys erasing the numbers, and continues the procedure until only one number is left on the whiteboard. What number is it?

Three tablespoons of milk from a glass of milk are poured into a glass of tea, and the liquid is thoroughly mixed. Then three tablespoons of this mixture are poured back into the glass of milk. Which is greater now: the percentage of milk in the tea or the percentage of tea in the milk?

Louise has a chessboard \(8\times8\) without two opposite corners (see the picture), and 31 dominoes \(2\times1\). Can she tile the crippled chessboard with dominoes she got?

Numbers \(1,2,\dots,20\) are written on a whiteboard. In one go Louise is allowed to wipe out any two numbers \(a\) and \(b\), and write instead

(a) \(a+b-1\); (b) \(a\times b\).

As you already know, Louise enjoys erasing the numbers, and has fun until only one number is left on the whiteboard. What number is it?

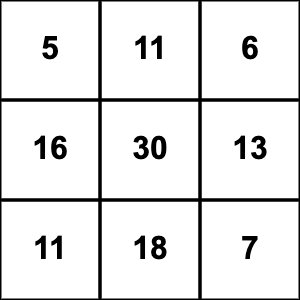
There is a \(3 \times 3\) grid filled with zeros. Louise is allowed to add 1 to each small square inside any \(2\times2\) grid. Can she ever get the following table as a result of her actions?

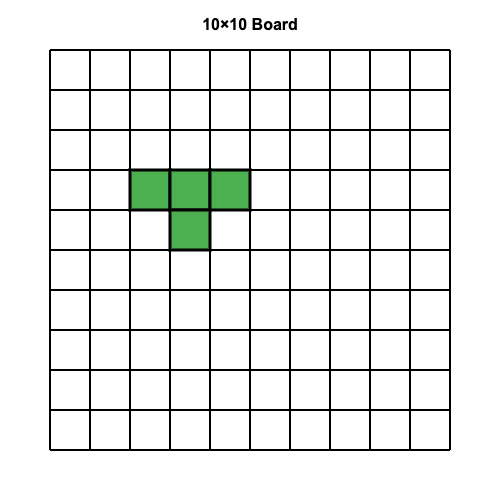
Prove that a \(10\times10\) board cannot be covered by T-shaped tiles (shown below)