Problems

For each pair of real numbers \(a\) and \(b\), consider the sequence of numbers \(p_n = \lfloor 2 \{an + b\}\rfloor\). Any \(k\) consecutive terms of this sequence will be called a word. Is it true that any ordered set of zeros and ones of length \(k\) is a word of the sequence given by some \(a\) and \(b\) for \(k = 4\); when \(k = 5\)?

Note: \(\lfloor c\rfloor\) is the integer part, \(\{c\}\) is the fractional part of the number \(c\).

Is there a sequence of natural numbers in which every natural number occurs exactly once, and for any \(k = 1, 2, 3, \dots\) the sum of the first \(k\) terms of the sequence is divisible by \(k\)?

Ten pairwise distinct non-zero numbers are such that for each two of them either the sum of these numbers or their product is a rational number.

Prove that the squares of all numbers are rational.

A convex figure and point \(A\) inside it are given. Prove that there is a chord (that is, a segment joining two boundary points of a convex figure) passing through point \(A\) and dividing it in half at point \(A\).

Author: A.K. Tolpygo

An irrational number \(\alpha\), where \(0 <\alpha <\frac 12\), is given. It defines a new number \(\alpha_1\) as the smaller of the two numbers \(2\alpha\) and \(1 - 2\alpha\). For this number, \(\alpha_2\) is determined similarly, and so on.

a) Prove that for some \(n\) the inequality \(\alpha_n <3/16\) holds.

b) Can it be that \(\alpha_n> 7/40\) for all positive integers \(n\)?

Numbers \(1,2,\dots,20\) are written on a whiteboard. In one go Louise is allowed to wipe out any two numbers \(a\) and \(b\), and write their sum \(a+b\) instead. Louise enjoys erasing the numbers, and continues the procedure until only one number is left on the whiteboard. What number is it?

Three tablespoons of milk from a glass of milk are poured into a glass of tea, and the liquid is thoroughly mixed. Then three tablespoons of this mixture are poured back into the glass of milk. Which is greater now: the percentage of milk in the tea or the percentage of tea in the milk?

Louise has an \(8\times 8\) chessboard with two opposite corners removes, just like in the picture below. She also has 31 \(2\times1\) dominoes. Can she tile this board with the dominoes she has?

Numbers \(1,2,\dots,20\) are written on a whiteboard. In one go Louise is allowed to wipe out any two numbers \(a\) and \(b\), and write instead

(a) \(a+b-1\); (b) \(a\times b\).

As you already know, Louise enjoys erasing the numbers, and has fun until only one number is left on the whiteboard. What number is it?

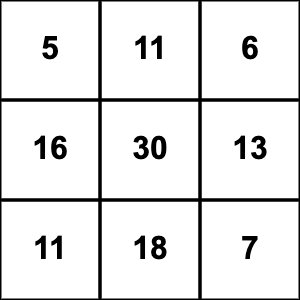
There is a \(3 \times 3\) grid filled with zeros. Louise is allowed to add 1 to each small square inside any \(2\times2\) grid. Can she ever get the following table as a result of her actions?