At a contest named “Ah well, monsters!”, 15 dragons stand in a row. Between neighbouring dragons the number of heads differs by 1. If the dragon has more heads than both of his two neighbors, he is considered cunning, if he has less than both of his neighbors – strong, the rest (including those standing at the edges) are considered ordinary. In the row there are exactly four cunning dragons – with 4, 6, 7 and 7 heads and exactly three strong ones – with 3, 3 and 6 heads. The first and last dragons have the same number of heads.
a) Give an example of how this could occur.
b) Prove that the number of heads of the first dragon in all potential examples is the same.
There are three piles of rocks: in the first pile there are 10 rocks, 15 in the second pile and 20 in the third pile. In this game (with two players), in one turn a player is allowed to divide one of the piles into two smaller piles. The loser is the one who cannot make a move. Which player would be the winner?
Numbers \(1,2,\dots,20\) are written on a whiteboard. In one go Louise is allowed to wipe out any two numbers \(a\) and \(b\), and write their sum \(a+b\) instead. Louise enjoys erasing the numbers, and continues the procedure until only one number is left on the whiteboard. What number is it?
Three tablespoons of milk from a glass of milk are poured into a glass of tea, and the liquid is thoroughly mixed. Then three tablespoons of this mixture are poured back into the glass of milk. Which is greater now: the percentage of milk in the tea or the percentage of tea in the milk?
Louise has a chessboard \(8\times8\) without two opposite corners (see the picture), and 31 dominoes \(2\times1\). Can she tile the crippled chessboard with dominoes she got?
Numbers \(1,2,\dots,20\) are written on a whiteboard. In one go Louise is allowed to wipe out any two numbers \(a\) and \(b\), and write instead
(a) \(a+b-1\); (b) \(a\times b\).
As you already know, Louise enjoys erasing the numbers, and has fun until only one number is left on the whiteboard. What number is it?
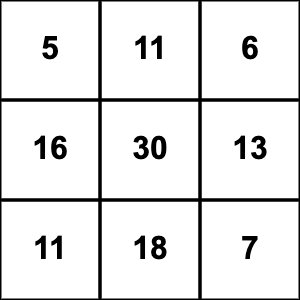
There is a \(3 \times 3\) grid filled with zeros. Louise is allowed to add 1 to each small square inside any \(2\times2\) grid. Can she ever get the following table as a result of her actions?
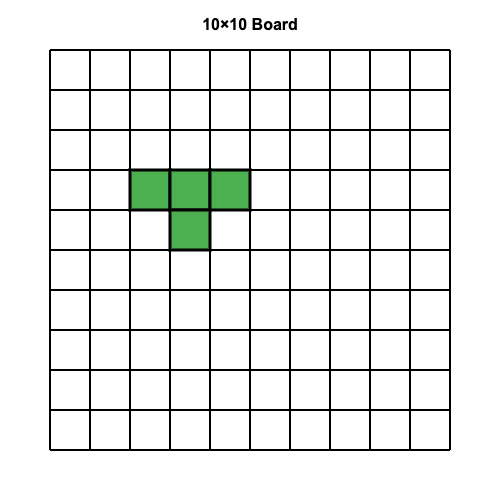
Prove that a \(10\times10\) board cannot be covered by T-shaped tiles (shown below)
Zara has an \(8\times8\) chessboard, in the usual coloring. She can repaint all the squares of a row or column, i.e., all white squares become black, and all black squares become white. Can she get exactly one black square?
A rectangular floor is to be covered by \(2 \times 2\) and \(1\times4\) tiles (everything is arranged). Unfortunately one tile got smashed, but we have one more tile of the other kind available. Can we retile the floor perfectly?