Problems

Cut a square into three parts and then use these three pieces to form a triangle such that:

1. All its angles are acute (i.e: less than \(90^\circ\)).

2. All its sides are of different lengths.

The Pythagorean Theorem is one of the most important facts about geometry. It says that if we have a right-angled triangle (i.e: it has an angle of \(90^\circ\)), whose longest side measures \(C\), and its other two other sides measure \(A\) and \(B\):

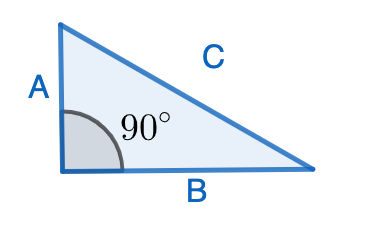
then \(A^2+B^2=C^2\). There are many proofs of this fact, and some involve dissections! Let’s have a look at the following two ways to dissect the same square:

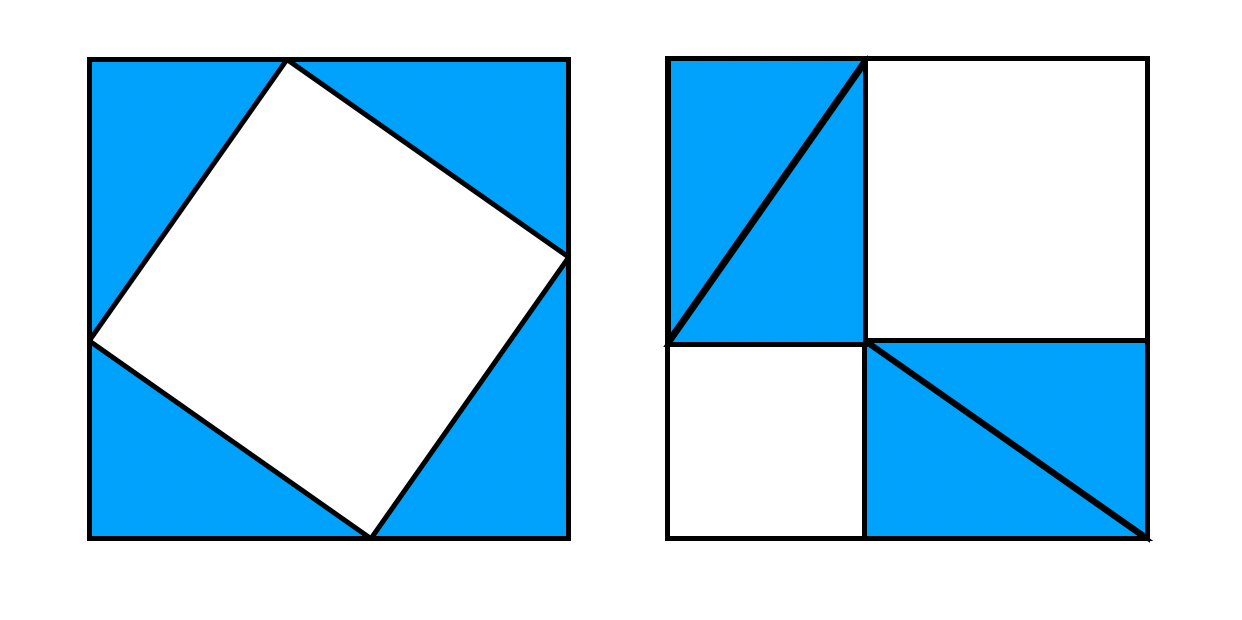
Can you explain how these dissections prove the Pythagorean Theorem?