Problems

Kate and Gina agreed to meet at the underground in the first hour of the afternoon. Kate comes to the meeting place between noon and one o’clock in the afternoon, waits for 10 minutes and then leaves. Gina does the same.

a) What is the probability that they will meet?

b) How will the probability of a meeting change if Gina decides to come earlier than half past twelve, and Kate still decides to come between noon and one o’clock?

c) How will the probability of a meeting change if Gina decides to come at an arbitrary time between 12:00 and 12:50, and Kate still comes between 12:00 and 13:00?

The upper side of a piece of square paper is white, and the lower one is red. In the square, a point F is randomly chosen. Then the square is bent so that one randomly selected vertex overlaps the point F. Find the mathematical expectation of the number of sides of the red polygon that appears.

At a factory known to us, we cut out metal disks with a diameter of 1 m. It is known that a disk with a diameter of exactly 1 m weighs exactly 100 kg. During manufacturing, a measurement error occurs, and therefore the standard deviation of the radius is 10 mm. Engineer Gavin believes that a stack of 100 disks on average will weigh 10,000 kg. By how much is the engineer Gavin wrong?

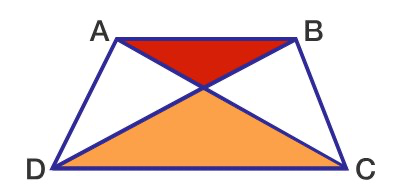
The area of the red triangle is \(25\) and the area of the orange triangle is \(49\). What is the area of the trapezium \(ABCD\)?

Prove that the relation between areas of two similar polygons equals to the square of their similarity coefficient.