Problems

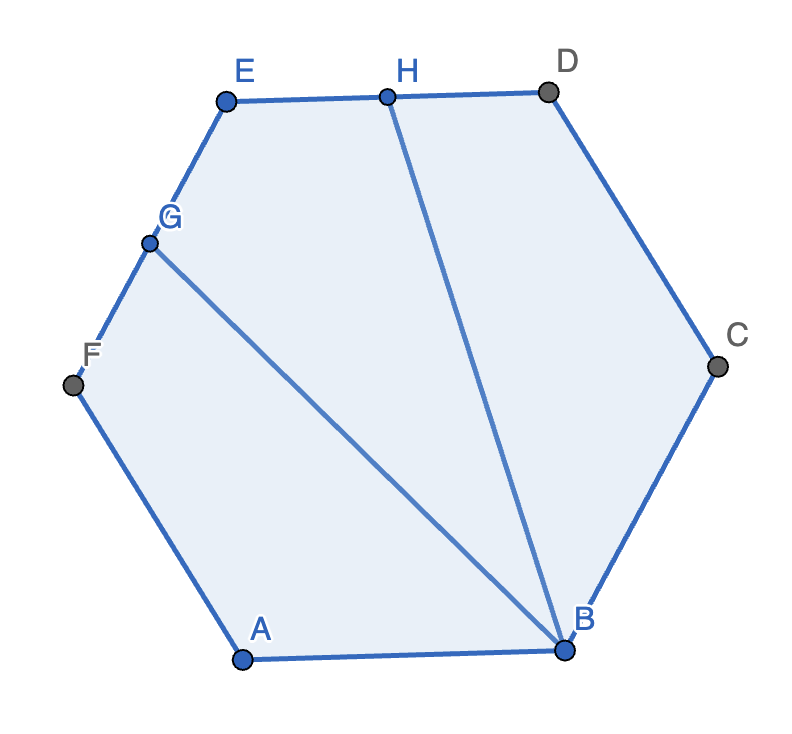
Let \(ABCDEF\) be a regular hexagon. Points \(G\) and \(H\) lie on \(EF\) and \(DE\) respectively such that \(|EG|=|EH|\). Furthermore, the area of quadrilateral \(ABGF\) is equal to the area of quadrilateral \(BGEH\), which are both equal to the area of \(BCDH\). What’s the ratio \(\frac{|EG|}{|EF|}\)?

In the diagram, all the small squares are of the same size. What fraction of the large square is shaded?

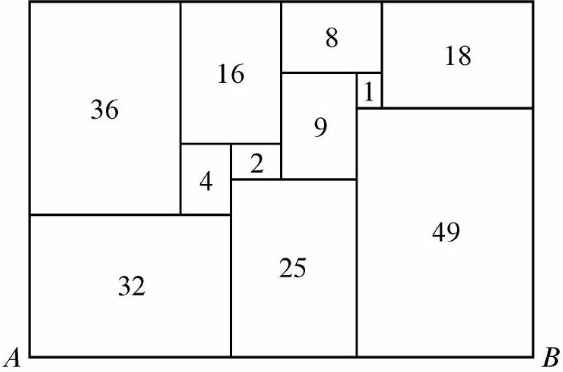
All of the rectangles in the figure below, which is drawn to scale, are similar to the big rectangle (that is, their sides are in the same ratio). Each number represents the area of the rectangle. What is the length \(AB\)?

We ‘typically’ use the formula \(\frac{1}{2}bh\) for the area of a triangle, where \(b\) is the length of the base, and \(h\) is the perpendicular height. Here’s another one, called Heron’s formula.

Call the sides of the triangle \(a\), \(b\) and \(c\). The perimeter is \(a+b+c\). We call half of this the semiperimeter, \(s=\frac{a+b+c}{2}\). Then the area of this triangle is \[\sqrt{s(s-a)(s-b)(s-c)}.\] Prove this formula is correct.