Problems

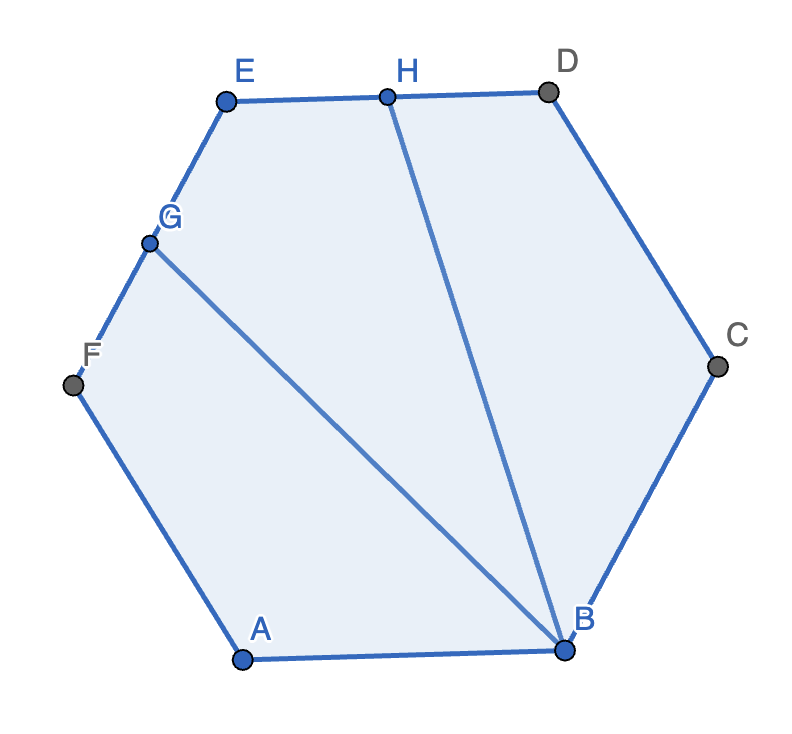
Let \(ABCDEF\) be a regular hexagon. Points \(G\) and \(H\) lie on \(EF\) and \(DE\) respectively such that \(|EG|=|EH|\). Furthermore, the area of quadrilateral \(ABGF\) is equal to the area of quadrilateral \(BGEH\), which are both equal to the area of \(BCDH\). What’s the ratio \(\frac{|EG|}{|EF|}\)?

In the diagram, all the small squares are of the same size. What fraction of the large square is shaded?

A simple polygon is a polygon that does not intersect itself and has no holes. Suppose we have a simple polygon \(S\) whose vertices consists of only integer coordinates.

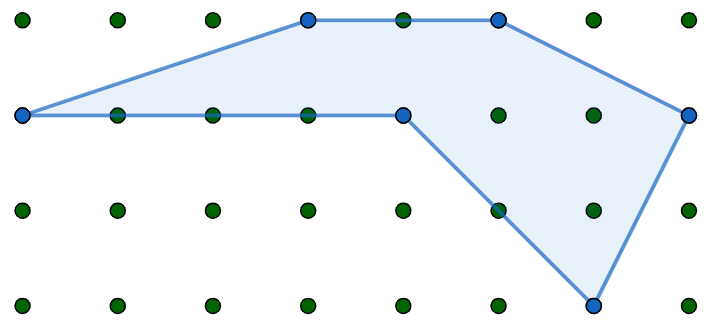
The area turns out to be remarkably easy to calculate. Count up the number of points with integer coordinate inside the polygon and on the boundary; call them \(i\) and \(b\) respectively. The area is then \[A(S) = i+\frac{b}{2}-1.\]

In the picture above, \(i=3\) and \(b=11\), so \(A(S) = \frac{15}{2}\). Prove that this formula for the area \(A(S)\) is correct.