Problems

In the picture below you can see the graphs of \(K_5\), the complete graph on \(5\) vertices, and \(K_{3,3}\), the complete bipartite graph on \(3\) and \(3\) vertices. A theorem states that these graphs cannot be embedded into plane, namely one cannot draw graphs \(K_5\) and \(K_{3,3}\) on a plane in such a way that there are no intersecting edges.
The question is: can you draw the graphs \(K_5\) and \(K_{3,3}\) without intersecting edges on a torus?

If we glue the opposite sides of the paper band in the same direction as on the picture, we will get a cylinder. What surface do we get, if we glue the circles of the cylinder in the same direction as well?

We start with a rectangular sheet of paper - preferably with proportions more than \(6:1\), so that it looks more like a band. For now assume that one can stretch or shrink the paper band as needed. Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the opposite direction as in the picture.

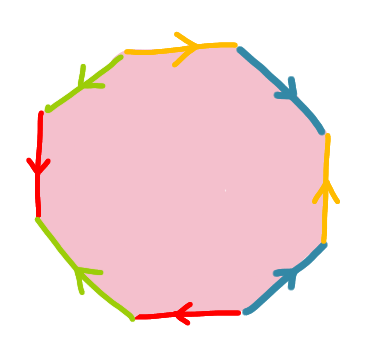
How would you describe the surface obtained by glueing the sides of the octagon as on the picture? Sides of the same colour are glued together in the same direction as shown.

Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.

Describe the surface which we can get if we start with a rectangular sheet of paper, make a Moebius band by glueing the opposite sides in the opposite directions and then glue the other opposite sides of the paper band in the opposite direction as on the picture.

Suppose you have a coffee mug made of stretchy and expandable material. How do you mold it into a donut that has a hole inside?

Take a straight string of finite length. Put the right half on top of the left half to form a hoop, and then pass it (the piece now on top) through the hoop from underneath. Glue the two ends together to form the trefoil knot.

Draw a sequence of pictures to illustrate the formation of the trefoil knot.

In the picture below, each side is glued in the same direction as its opposite side. Draw a sequence of pictures to show the gluing process and the final shape.

Take a straight string of finite length. Wrap the right half over and then under the left half so that it is pointing to the right again and there is a hoop. Pass the right pointing piece through the hoop from above. Glue the two ends together to form the figure-8 knot.

Draw a sequence of pictures to illustrate the formation of the figure-8 knot, seen below.