Problems

The White Rook pursues a black horse on a board of \(3 \times 1969\) cells (they walk in turn according to the usual rules). How should the rook play in order to take the horse? White makes the first move.

This problem is from Ancient Rome.

A rich senator died, leaving his wife pregnant. After the senator’s death it was found out that he left a property of 210 talents (an Ancient Roman currency) in his will as follows: “In the case of the birth of a son, give the boy two thirds of my property (i.e. 140 talents) and the other third (i.e. 70 talents) to the mother. In the case of the birth of a daughter, give the girl one third of my property (i.e. 70 talents) and the other two thirds (i.e. 140 talents) to the mother.”

The senator’s widow gave birth to twins: one boy and one girl. This possibility was not foreseen by the late senator. How can the property be divided between three inheritors so that it is as close as possible to the instructions of the will?

Two play a game on a chessboard \(8 \times 8\). The player who makes the first move puts a knight on the board. Then they take turns moving it (according to the usual rules), whilst you can not put the knight on a cell which he already visited. The loser is one who has nowhere to go. Who wins with the right strategy – the first player or his partner?

During the ball every young man danced the waltz with a girl, who was either more beautiful than the one he danced with during the previous dance, or more intelligent, but most of the men (at least 80%) – with a girl who was at the same time more beautiful and more intelligent. Could this happen? (There was an equal number of boys and girls at the ball.)

Imagine an infinitely large sheet of paper with a square drawn on it. Somewhere on the paper, a point \(P\) is marked with ink that is invisible to you. However, a friend with a special pair of glasses can see the point.

We are allowed to draw straight lines on the paper, and for each line, our friend will tell us on which side of the line the point \(P\) is. (If \(P\) is exactly on the line, they will say so.) For example, on this picture, our friend would say that the point \(P\) is above the line we’ve drawn:

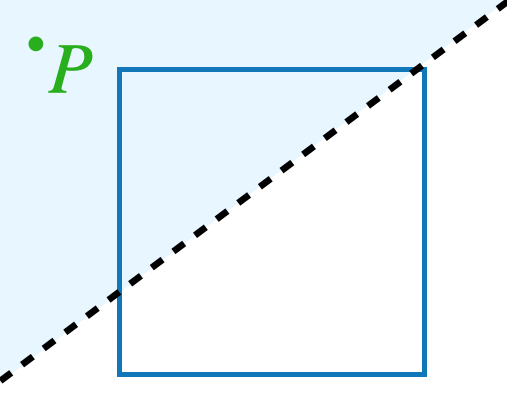
What is the smallest number of such questions that are needed in order to be certain whether \(P\) lies inside the square? Explain why it cannot be done in less questions then you are suggesting.

Take any two non-equal numbers \(a\) and \(b\), then we can write \[a^2 - 2ab + b^2 = b^2 - 2ab + a^2\] Using the formula \((x-y)^2 = x^2 - 2xy + y^2\), we complete the squares and rewrite the equality above as \[(a-b)^2 = (b-a)^2.\] As we take a square root from the both sides of the equality, we get \[a-b = b-a.\] Finally, adding to both sides \(a+b\) we get \[\begin{aligned} a-b + (a+b) &= b-a + (a+ b)\\ 2a&= 2b\\ a&=b. \end{aligned}\] Therefore, All NON-EQUAL NUMBERS ARE EQUAL! (This is gibberish, isn’t it?)

Consider equation \[x-a=0\] Dividing both sides of this equation by \(x-a\), we get \[\frac{x-a}{x-a} = \frac{0}{x-a}.\] But \(\frac{x-a}{x-a}=1\) and \(\frac{0}{x-a}=0\). Therefore, we get \[1=0.\]

Let \(n\) be some positive number. It is obvious that \[2n-1<2n.\] Take another positive number \(a\), and multiply both sides of the inequality by \((-a)\) \[-2na +a< -2na.\] Now, subtracting \((-2na)\) from both sides of the inequality we get \(a<0\).

Thus, ALL POSITIVE NUMBERS ARE NEGATIVE!

Suppose \(a \neq b\). We can write \[-a = b - (a+b)\] and \[-b = a - (a+b)\] Since \((-a)b = a(-b)\), then \[( b - (a+b))b = a(a - (a+b))\] Removing the brackets, we have \[b^2 - (a+b)b = a^2 - a(a+b)\] Adding \(\left(\frac{a+b}{2}\right)^2\) to each member of the equality we may complete the square of the differences of two numbers \[\left(b - \frac{a+b}{2}\right)^2 = \left(a - \frac{a+b}{2}\right)^2\] From the equality of the squares we conclude the equality of the bases \[b - \frac{a+b}{2} = a - \frac{a+b}{2}.\] Adding \(\frac{a+b}{2}\) to both sides of equality we get \(a=b\). Therefore, WE HAVE SHOWED THAT FROM \(a\neq b\) IT FOLLOWS \(a=b\).

Let \(x\) be equal to 1. Then we can write \(x^2=1\), or putting it differently \(x^2 -1 =0\). By using the difference of two squares formula we get \[(x+1)(x-1)=0\] Dividing both sides of the equality by \(x-1\) we obtain \[x+1=0,\] in other words \(x=-1\). But earlier we assumed \(x=1\). THUS \[-1=1\ !\]