Problems

During the ball every young man danced the waltz with a girl, who was either more beautiful than the one he danced with during the previous dance, or more intelligent, but most of the men (at least 80%) – with a girl who was at the same time more beautiful and more intelligent. Could this happen? (There was an equal number of boys and girls at the ball.)

Imagine an infinitely large sheet of paper with a square drawn on it. Somewhere on the paper, a point \(P\) is marked with ink that is invisible to you. However, a friend with a special pair of glasses can see the point.

We are allowed to draw straight lines on the paper, and for each line, our friend will tell us on which side of the line the point \(P\) is. (If \(P\) is exactly on the line, they will say so.) For example, on this picture, our friend would say that the point \(P\) is above the line we’ve drawn:

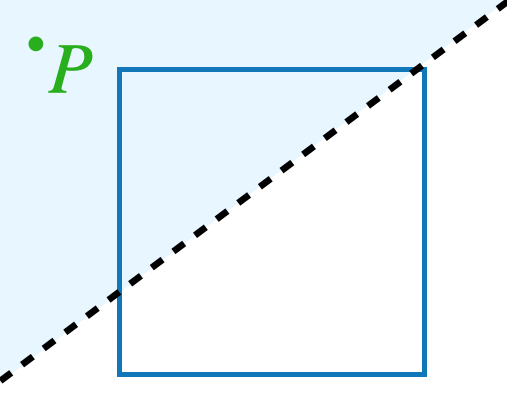
What is the smallest number of such questions that are needed in order to be certain whether \(P\) lies inside the square? Explain why it cannot be done in less questions then you are suggesting.

Ten little circles are drawn on the following \(4\times 4\) board:

Is it possible to cut the board into four identical parts, in such a way that each part contains 1, 2, 3, and 4 circles correspondingly?

Cut a square into a heptagon (7 sides) and an octagon (8 sides) in such a way, that for every side of an octagon there exists an equal side belonging to the heptagon.

Sometimes life can make us do the craziest of things. In this problem you just need to find out how one can cut an \(8\times8\) chessboard into 20 pieces each having the same perimeter and consisting of a whole number of cells.

Cut a rectangle into two identical pentagons.

(a) Cut the rectangle into two identical quadrilaterals.

(b) Cut the rectangle into two identical hexagons.

(c) Cut the rectangle into two identical heptagons.

Can one cut a square into (a) one 30-gon and five pentagons? (b) one 33-gon and three 10-gons?

Can Jennifer draw an octagon and a line passing through two of its vertices in such a way that this line cuts a 10-gon from it?

How can you divide a pancake with three straight sections into 4, 5, 6, 7 parts?