Problems
There are 13 weights. It is known that any 12 of them could be placed in 2 scale cups with 6 weights in each cup in such a way that balance will be held.
Prove the mass of all the weights is the same, if it is known that:
a) the mass of each weight in grams is an integer;
b) the mass of each weight in grams is a rational number;
c) the mass of each weight could be any real (not negative) number.
Two weighings. There are 7 coins which are identical on the surface, including 5 real ones (all of the same weight) and 2 counterfeit coins (both of the same weight, but lighter than the real ones). How can you find the 3 real coins with the help of two weighings on scales without weights?
In the rebus below, replace the letters with numbers such that the same numbers are represented with the same letter. The asterisks can be replaced with any numbers such that the equations hold.
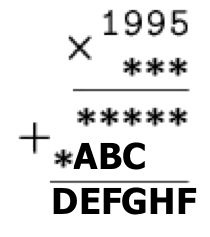
An explanation of the notation used: the unknown numbers in the third and fourth rows are the results of multiplying 1995 by each digit of the number in the second row, respectively. These third and fourth rows are added together to get the total result of the multiplication \(1995 \times ***\), which is the number in the fifth row. This is an example of a “long multiplication table”.
Jessica, Nicole and Alex received 6 coins between them: 3 gold coins and 3 silver coins. Each of them received 2 coins. Jessica doesn’t know which coins the others received but only which coins she has. Think of a question which Jessica can answer with either “yes”, “no” or “I don’t know” such that from the answer you can know which coins Jessica has.
There are \(12\) aliens in the High Council of the planet of liars and truth tellers. “There is no-one honest here,” said the first member of the council. “There is at most one honest person here,” said the second person. The third person said that there are at most \(2\) honest members, the fourth person said there are at most \(3\) honest aliens, and so on until the twelfth person, who said there are at most \(11\) honest aliens. How many honest members are in the High Council?
In a class there are 50 children. Some of the children know all the letters except “h” and they miss this letter out when writing. The rest know all the letters except “c” which they also miss out. One day the teacher asked 10 of the pupils to write the word “cat”, 18 other pupils to write “hat” and the rest to write the word “chat”. The words “cat” and “hat” each ended up being written 15 times. How many of the pupils wrote their word correctly?
Peter has 28 classmates. Each 2 out of these 28 have a different number of friends in the class. How many friends does Peter have?
A number set \(M\) contains \(2003\) distinct positive numbers, such that for any three distinct elements \(a, b, c\) in \(M\), the number \(a^2 + bc\) is rational. Prove that we can choose a natural number \(n\) such that for any \(a\) in \(M\) the number \(a\sqrt{n}\) is rational.
One day all the truth tellers on the planet decided to carry a clearly visible mark of truth in order to be distinguished from liars. Two truth tellers and two liars met and looked at each other. Which of them could say the phrase:
“All of us are truth tellers.”
“Only one of you is a truth teller.”
“Exactly two of you are truth tellers.”
Four numbers (from 1 to 9) have been used to create two numbers with four-digits each. These two numbers are the maximum and minimum numbers, respectively, possible. The sum of these two numbers is equal to 11990. What could the two numbers be?