Problems

A \(1 \times 10\) strip is divided into unit squares. The numbers \(1, 2, \dots , 10\) are written into squares. First, the number 1 is written in one square, then the number 2 is written into one of the neighboring squares, then the number 3 is written into one of the neighboring squares of those already occupied, and so on (the choice of the first square is made arbitrarily and the choice of the neighbor at each step). In how many ways can this be done?

A game takes place on a squared \(9 \times 9\) piece of checkered paper. Two players play in turns. The first player puts crosses in empty cells, its partner puts noughts. When all the cells are filled, the number of rows and columns in which there are more crosses than zeros is counted, and is denoted by the number \(K\), and the number of rows and columns in which there are more zeros than crosses is denoted by the number \(H\) (18 rows in total). The difference \(B = K - H\) is considered the winnings of the player who goes first. Find a value of B such that

1) the first player can secure a win of no less than \(B\), no matter how the second player played;

2) the second player can always make it so that the first player will receive no more than \(B\), no matter how he plays.

Does there exist an irreducible tiling with \(1\times2\) rectangles of a \(4\times 6\) rectangle?

Irreducibly tile a floor with \(1\times2\) tiles in a room that is a \(5\times8\) rectangle.

Tile the whole plane with the following shapes:

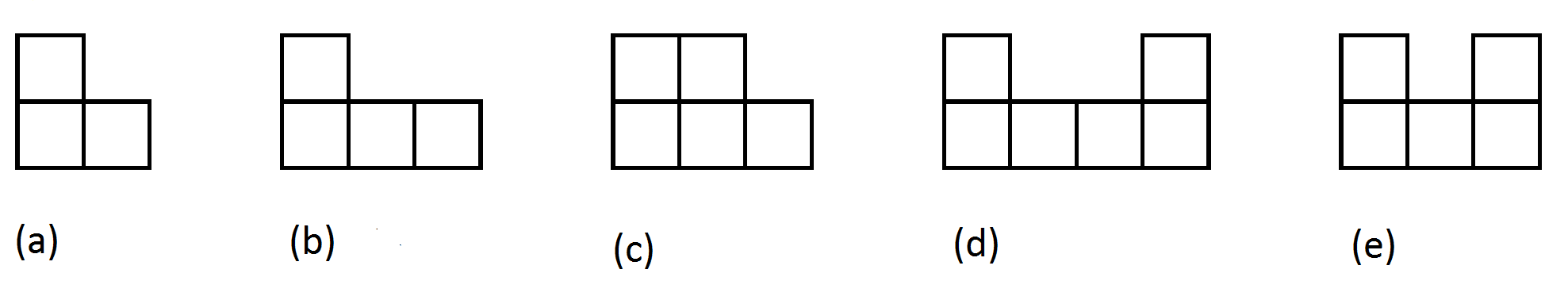
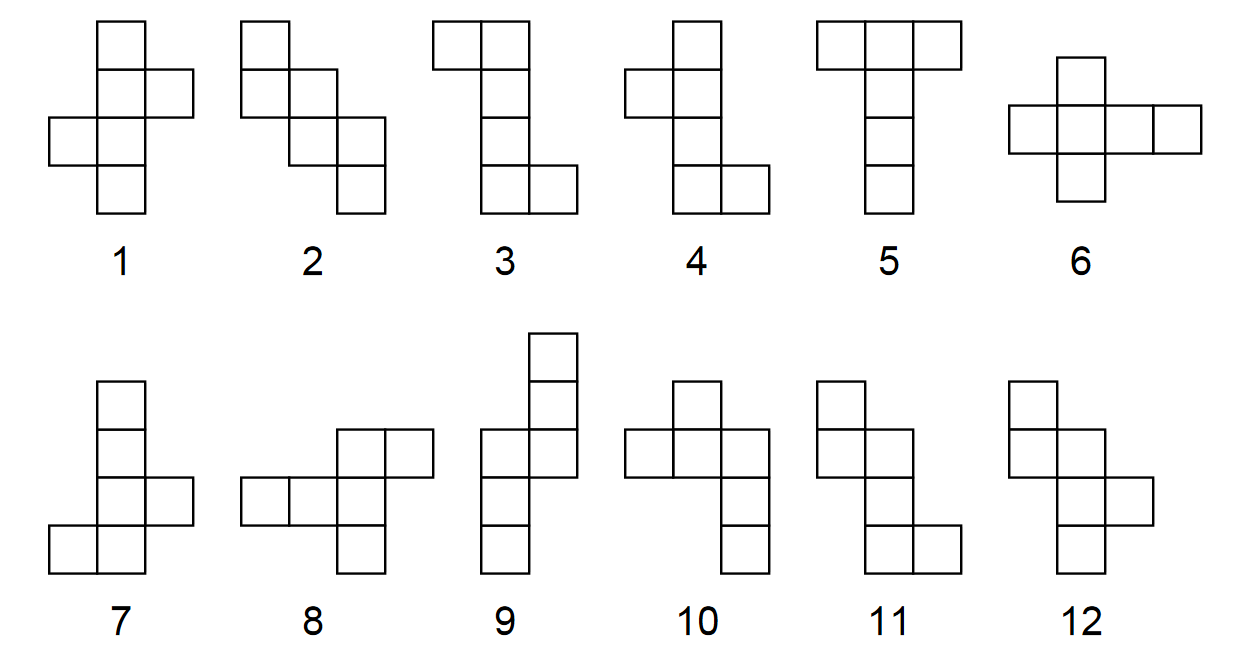
David Smith cut out 12 nets. He claimed that it was possible to make a cube out of each net. Roger Penrose looked at the patterns, and after some considerable thought decided that he was able to make cubes from all the nets except one. Can you figure out which net cannot make a cube?

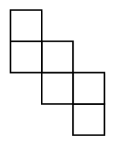
It is known that it is possible to cover the plane with any cube’s net. Show how you can cover the plane with this net:

In how many ways can you rearrange the numbers 1, 2, ..., 100 so the neighbouring numbers differ by not more than 1?

A strange wonderland creature is called a painting chameleon. If the queen puts the painting chameleon on a chess-like board then he moves one square at a time along the board either horizontally or vertically. When he moves, he either changes his colour to the colour of the square he moves to, or he paints the square he moves to into his own colour. The queen puts a white painting chameleon on an all-black board \(8\times8\) and orders the chameleon to paint the board into a chessboard. Can he succeed?

After removing a \(1\times 1\) square from the corner of a \(4\times 4\) square, we are left with the following shape:

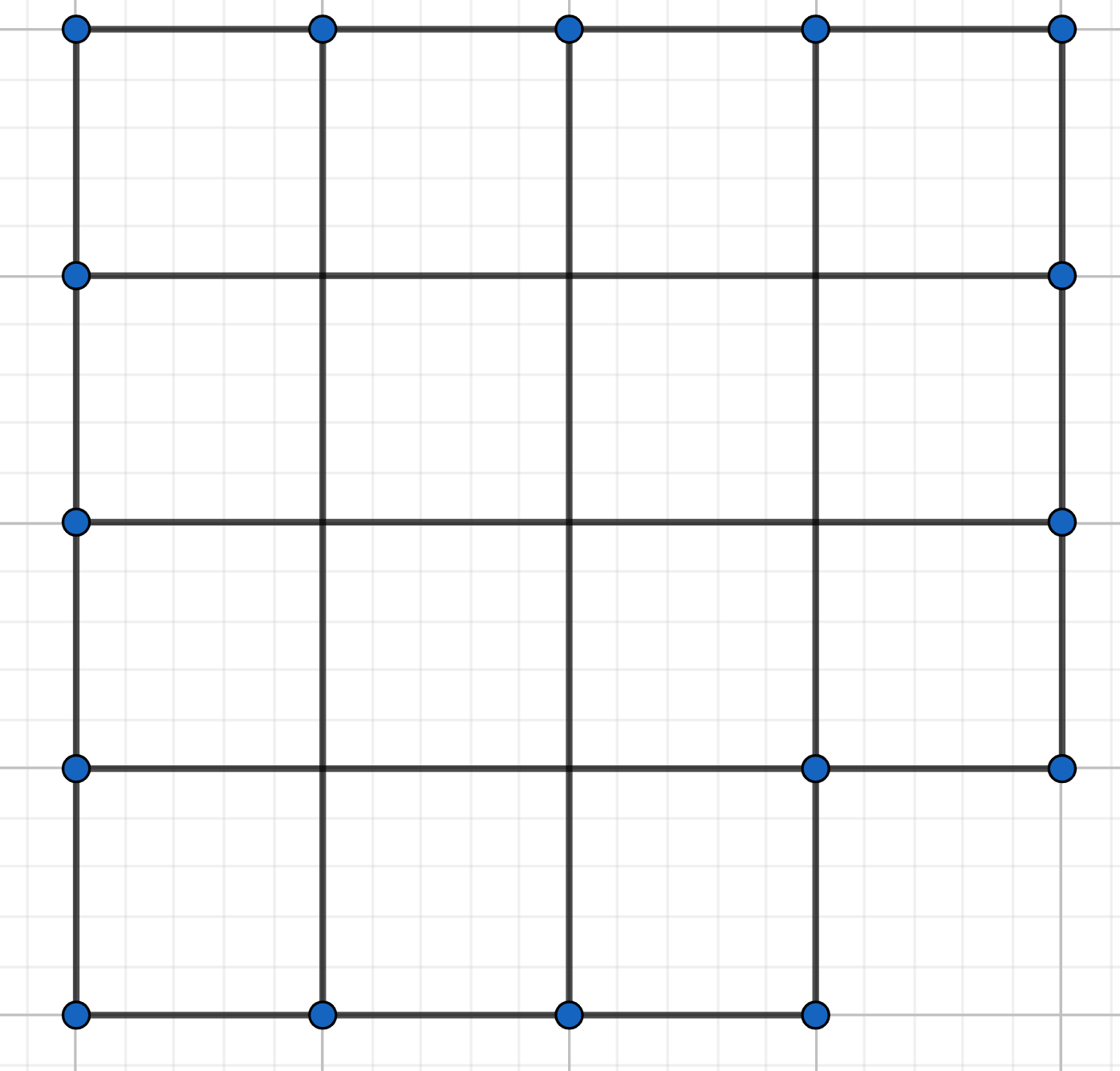
how can we cut this into three congruent shapes?