Problems

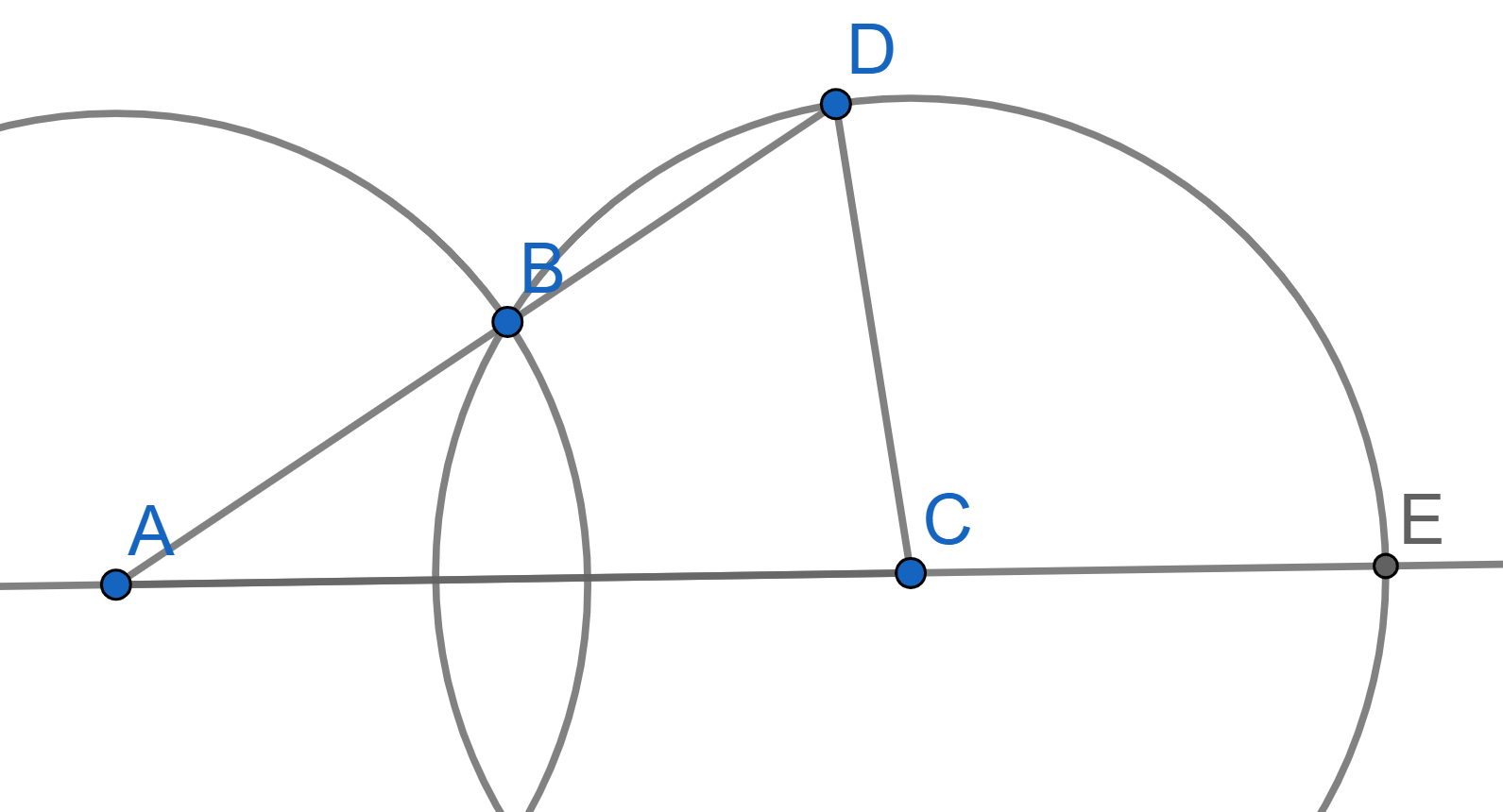
Two intersecting circles of radius \(R\) are given, and the distance between their centers is greater than \(R\). Prove that \(\angle ECD = 3\angle CAD\).

On the sides \(AB\), \(BC\) and \(AC\) of the triangle \(ABC\) points \(P\), \(M\) and \(K\) are chosen so that the segments \(AM\), \(BK\) and \(CP\) intersect at one point and \[\vec{AM} + \vec{BK}+\vec{CP} = 0\] Prove that \(P\), \(M\) and \(K\) are the midpoints of the sides of the triangle \(ABC\).