Problems

Cut the interval \([-1, 1]\) into black and white segments so that the integrals of any a) linear function; b) a square trinomial in white and black segments are equal.

Peter has 28 classmates. Each 2 out of these 28 have a different number of friends in the class. How many friends does Peter have?

\(x_1\) is the real root of the equation \(x^2 + ax + b = 0\), \(x_2\) is the real root of the equation \(x^2 - ax - b = 0\).

Prove that the equation \(x^2 + 2ax + 2b = 0\) has a real root, enclosed between \(x_1\) and \(x_2\). (\(a\) and \(b\) are real numbers).

With a non-zero number, the following operations are allowed: \(x \rightarrow \frac{1+x}{x}\), \(x \rightarrow \frac{1-x}{x}\). Is it true that from every non-zero rational number one can obtain each rational number with the help of a finite number of such operations?

At all rational points of the real line, integers are arranged. Prove that there is a segment such that the sum of the numbers at its ends does not exceed twice the number on its middle.

Prove that for any positive integer \(n\) the inequality

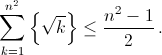
is true.

Find the sum \(1/3 + 2/3 + 2^2/3 + 2^3/3 + \dots + 2^{1000}/3\).

A number set \(M\) contains \(2003\) distinct positive numbers, such that for any three distinct elements \(a, b, c\) in \(M\), the number \(a^2 + bc\) is rational. Prove that we can choose a natural number \(n\) such that for any \(a\) in \(M\) the number \(a\sqrt{n}\) is rational.

A numeric set \(M\) containing 2003 distinct numbers is such that for every two distinct elements \(a, b\) in \(M\), the number \(a^2+ b\sqrt 2\) is rational. Prove that for any \(a\) in \(M\) the number \(q\sqrt 2\) is rational.

Does there exist a function \(f (x)\) defined for all \(x \in \mathbb{R}\) and for all \(x, y \in \mathbb{R}\) satisfying the inequality \(| f (x + y) + \sin x + \sin y | < 2\)?