Problems
Most magic tricks rely on some kind of sleight of hand. However, some tricks are powered by maths!
A fruitful way of analyzing card shuffles is by using the idea of “permutations". Permutations are important objects that occur in various parts of maths. Many interesting patterns emerge, and we will only touch the tip of the iceberg today.
Suppose you have a set of ordered objects. A permutation of this set is a reordering of the objects. For example, a permutation of a deck of cards ordered from top to bottom is simply a shuffle of the cards. Note that in general, a permutation can be defined as a relabelling of objects, so an order is not necessary.
Let’s discuss two ways of writing permutations.
The first way is two-line notation. Say you have the cards from top to bottom Ace, two, three. Say Ace is 1. Suppose that after a shuffle \(p\), we have from top to bottom two, three, Ace. The two-line notation keeps the original positions on the first line and the new positions in the second line.
\[p = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right).\]
A second way of writing permutations is function notation. In the same situation, we could write \(p(1)=3\), \(p(2)=1\) and \(p(3)=2\).
As a first indication of why permutations give a useful perspective, we note that permutations can be done after another and the result is still a permutation. Let \(q\) be the permutation on the same three cards given by \(q(1)=2\), \(q(2)=3\) and \(q(3)=1\). Consider \(qp\) which is performing \(p\) first and then \(q\). To find out what the effect of this composite permutation is on \(1\), we can visualize it as follows: \[1\mapsto3=p(1)\mapsto q(p(1))=q(3)=1.\]
This shows that the function notation plays very nicely with composing permutations. By the way, if we work out the entire \(qp\) in this fashion, we find that \[qp = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right).\]
In other words, \(q\) has “negated" the effect of \(p\)!
Certain geometric objects nicely blend when they happen to be
together in a problem. One possible example of such a pair of objects is
a circle and an inscribed angle.
We will be using the following statements in the examples and
problems:
1. The supplementary angles (angles “hugging" a straight line) add up to
\(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
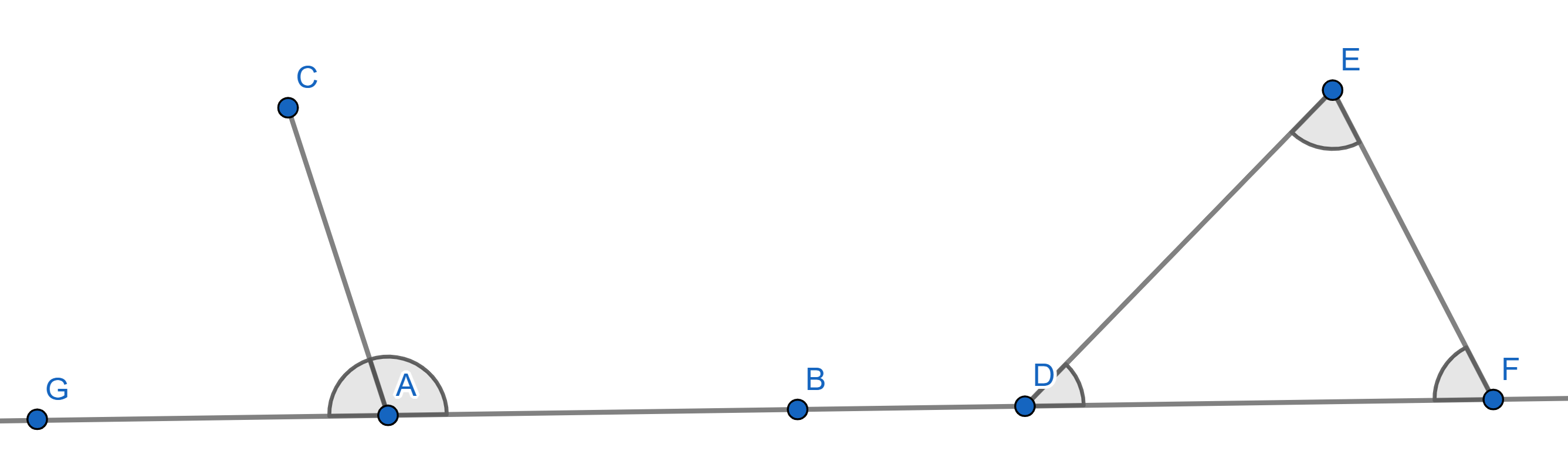
3. Two triangles are said to be “congruent" if ALL of their
corresponding sides and angles are equal.
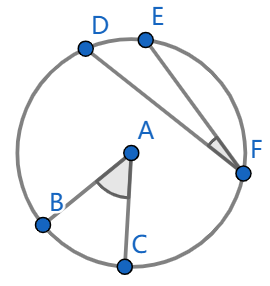
The following terminology will also be quite helpful. In the picture
below, the points \(B\) and \(C\) lie on the circumference of the circle
while the vertex \(A\) lies at the
centre of the circle. We say that the angle \(\angle BAC\) is a central angle.
The angle \(\angle DFE\) is called an
inscribed angle because the vertices \(D\), \(F\)
and \(E\) all lie on the circumference
of the circle.
Today we explore inequalities related to mean values of a set of
positive real numbers. Let \(\{a_1,a_2,...,a_n\}\) be a set of \(n\) positive real numbers. Define:
Quadratic mean (QM) as \[\sqrt{\frac{a_1^2 + a_2^2 +
...a_n^2}{n}}\] Arithmetic mean (AM) as \[\frac{a_1 + a_2 + ...+a_n}{n}\]
Geometric mean (GM) as \[\sqrt[n]{a_1a_2...a_n}\] Harmonic
mean (HM) as \[\frac{n}{\frac{1}{a_1} + \frac{1}{a_2} + ...
\frac{1}{a_n}}.\] Then the following inequality holds: \[\sqrt{\frac{a_1^2 + a_2^2 + ...a_n^2}{n}} \geq
\frac{a_1 + a_2 + ...+a_n}{n} \geq \sqrt[n]{a_1a_2...a_n} \geq
\frac{n}{\frac{1}{a_1} + \frac{1}{a_2} + ... \frac{1}{a_n}}.\] We
will prove \(QM\geq AM\) and infer the
\(GM \geq HM\) part from \(AM \geq GM\) in the examples. However, the
\(AM\geq GM\) part itself is more
technical. The Mean Inequality is a well known theorem and you can use
it in solutions today and refer to it on olympiads.
As the title suggests, today we’re going to colour some (if not all!) points in the plane, using only a couple of colours. We’ll show that no matter how we do this colouring, we’re guaranteed to get some structure. When we say ‘the plane’, imagine a flat piece of paper extending infinitely far in every direction.
Let’s look at some examples!
We often think of symmetry as a property of shapes. Another way of thinking about it is as something you do to an object which keeps the object looking the same. The example you’ve likely met is reflection. The other one that we’ll consider today is rotation. An important feature is that we consider ‘doing nothing’ as a symmetry - we call this the identity.
Suppose you want to compute the sum \(1+2+\dots+n\) up to some positive integer \(n\). Then you discover a curious pattern:
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \(1+2+\dots+n\) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 |
| \(\frac{n(n+1)}{2}\) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 |
We may guess at this point \(1+2+\dots+n = \frac{n(n+1)}{2}\). How can we prove it? One way is to attack the problem step by step.
When \(n=1\), the sum is just \(1\) and \(\frac{1\times(1+1)}{2}=1\). So far so good.
When \(n=2\), the sum is \(1+2 = 3\) and \(\frac{2\times(2+1)}{2}=3\). We can also see this in another way. As we already noted, \(1 = \frac{1\times(1+1)}{2}\). This means \[1+2 = \frac{1\times (1+1)}{2} + 2 = \frac{1\times2+2\times2}{2} = \frac{(1+2)\times 2}{2} = \frac{2\times(2+1)}{2}.\]
When \(n=3\), we have already proved that \(1 + 2 = \frac{2\times(2+1)}{2}\), so \[1+2+3 = \frac{2\times (2+1)}{2} + 3 = \frac{2\times3+2\times3}{2} = \frac{(2+2)\times 3}{2} = \frac{3\times(3+1)}{2}.\]
When \(n=4\), we have already proved that \(1 + 2 + 3 = \frac{3\times(3+1)}{2}\), so \[1+2+3+4 = \frac{3\times (3+1)}{2} + 4 = \frac{3\times4+2\times4}{2} = \frac{(3+2)\times 4}{2} = \frac{4\times(4+1)}{2}.\]
When \(n=5\), we have already proved that \(1 + 2 + 3 + 4 = \frac{4\times(4+1)}{2}\), so ...
It starts getting a bit boring, but hopefully you get the point. Important takeaways from the example above:
The truth of the next case depends ONLY on the previous case.
We know what we need to prove IS true for the first case, that is \(n=1\).
By repeating the same procedure starting from \(n=1\), we can eventually reach any given positive integer.
Thus, the formula is true for all positive integers (also known as natural numbers).
A diagram summarizing the idea: \[\text{true for } n=1 \implies \text{true for } n=2 \implies \text{true for } n=3 \implies \text{true for } n=4 \implies \dots\]
This is the mechanism behind induction. Formally, we can state the principle of mathematical induction as follows. Suppose we have a series of statements numbered by the positive integers: 1st statement, 2nd statement, 3rd statement and so on. Suppose that
the 1st statement is true (the base case is true);
whenever the \(n\)th statement is true, the \((n+1)\)th statement is also true (the induction step is valid assuming the induction hypothesis).
Then the statement is true for all positive integers (natural numbers). Let us revisit the example and prove it formally now using the principle of mathematical induction.
You may have seen the pigeonhole principle before, sometimes called
Dirichlet’s box principle. It says that if you have more pigeons than
pigeonholes, and you put all of the pigeons into some pigeonhole, then
there exists at least one pigeonhole with at least two pigeons. While it
sounds quite simple, it’s a powerful technique. The difficult thing is
often choosing the appropriate pigeons and pigeonholes.
It has multiple applications in various situations.
Today we will see how to use it in geometric problems.
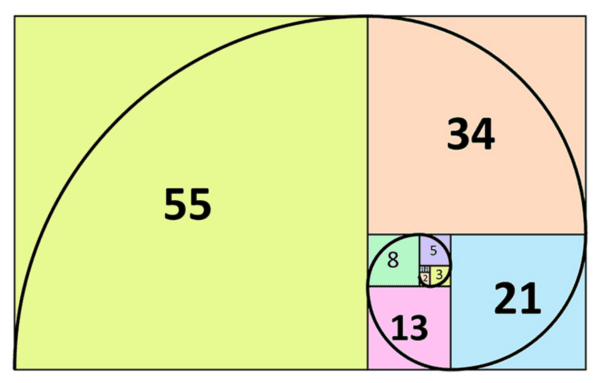
This week we’re looking at Fibonacci numbers, and other sequences of numbers.
We say that the ‘zeroth’ Fibonacci number is \(0\) and the first Fibonacci number is \(1\). Then, from that point, every Fibonacci number is found by adding the two previous Fibonacci numbers. This means that the sequence begins \(0,1,1,2,3,5,8,13,21,34,55,89,144,...\)
The Fibonacci numbers hide lots of patterns which we’ll explore today. The spiral below is formed by taking squares whose side lengths are Fibonacci numbers, and drawing quarter circles in each square.
Today we will be finding the areas of some geometric figures. Here is a brief reminder of how to calculate the area of common shapes.
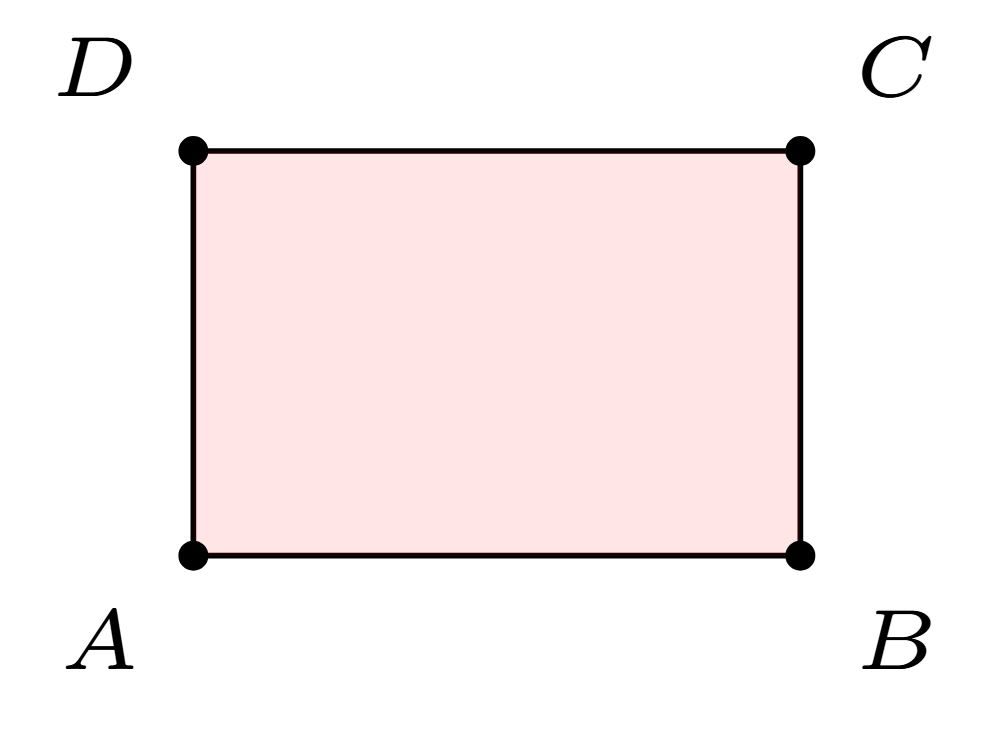
In the picture below, the area of the rectangle is \(|AB|\times |AD|\).
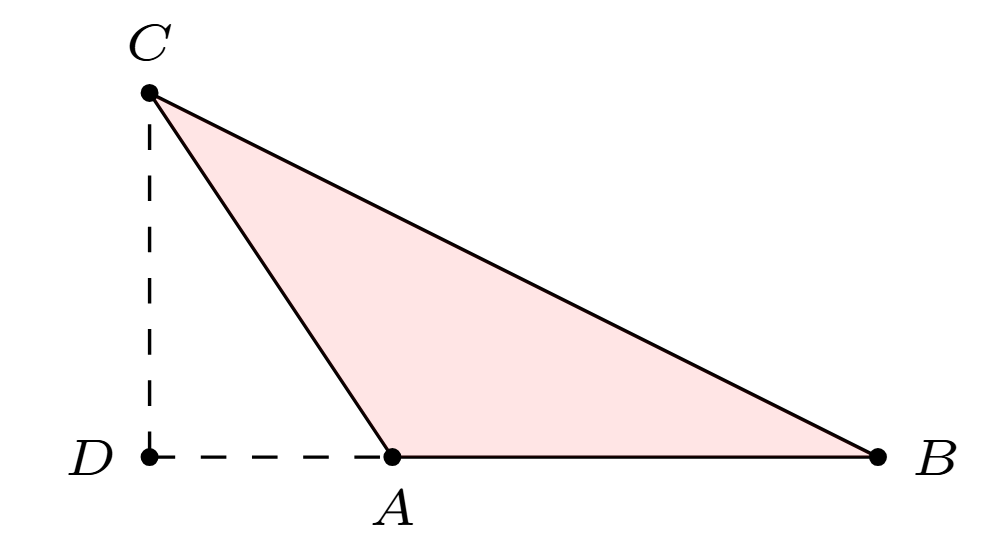
The area of a triangle is given by \(\frac{1}{2}bh\), where \(b\) is the length of a chosen base and \(h\) is the height. In this case, the segment \(AB\) is the base and \(CD\) is the altitude corresponding to the base \(AB\).
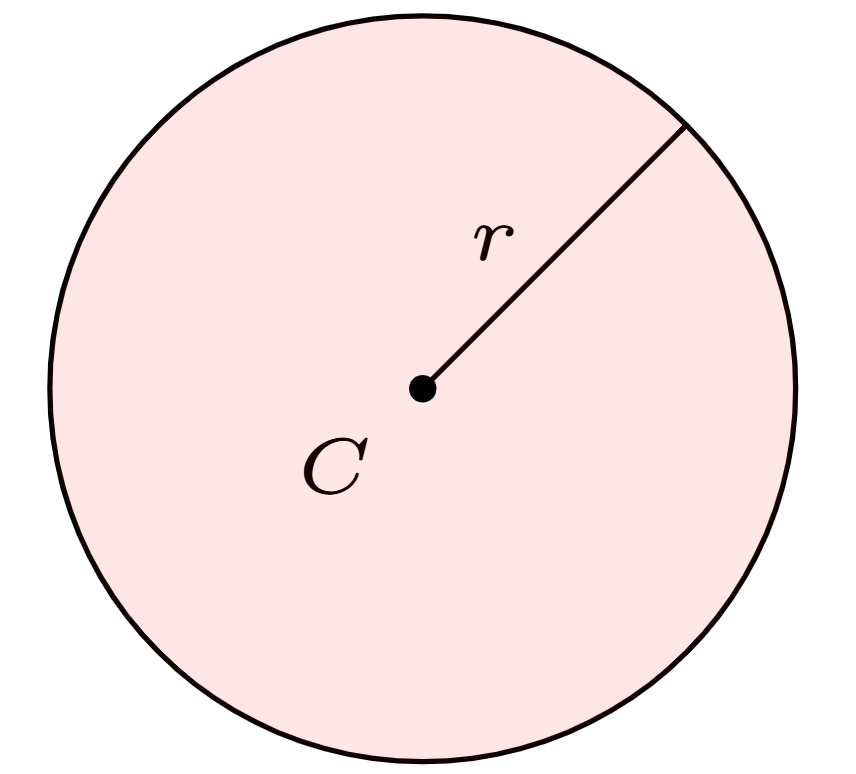
The area of a circle with radius \(r\) is \(\pi r^2\). The number \(\pi\) is approximately 3.14159 to five decimal points.
Diophantine equations are those where we’re only interested in finding the integer (whole number) solutions. Some of these equations are quite simple, while others look simple but are actually very difficult. The most famous one is Fermat’s Last Theorem, which says that when \(n>2\), there are no solutions to \[x^n+y^n=z^n.\] Pierre de Fermat claimed that he proved this in 1637, scribbling it in the margin of a book, but said “I have discovered a truly marvelous proof of this, which this margin is too narrow to contain." It was only proved by Andrew Wiles in 1995. Today’s problems won’t take 358 years to solve.