Problems

We call a triple of natural numbers (also known as positive integers) \((a,b,c)\) satisfying \(a^2+b^2=c^2\) a Pythagorean triple. If, further, \(a\), \(b\) and \(c\) are relatively prime, then we say that \((a,b,c)\) is a primitive Pythagorean triple.

Show that every primitive Pythagorean triple can be written in the form \((u^2-v^2,2uv,u^2+v^2)\) for some coprime positive integers \(u>v\).

What symmetries does a regular hexagon have, and how many?

Let \(X\) be a finite set, and let \(\mathcal{P}X\) be the power set of \(X\) - that is, the set of subsets of \(X\). For subsets \(A\) and \(B\) of \(X\), define \(A*B\) as the symmetric difference of \(A\) and \(B\) - that is, those elements that are in either \(A\) or \(B\), but not both. In formal set theory notation, this is \(A*B=(A\cup B)\backslash(A\cap B)\).

Prove that \((\mathcal{P}X,*)\) forms a group.

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

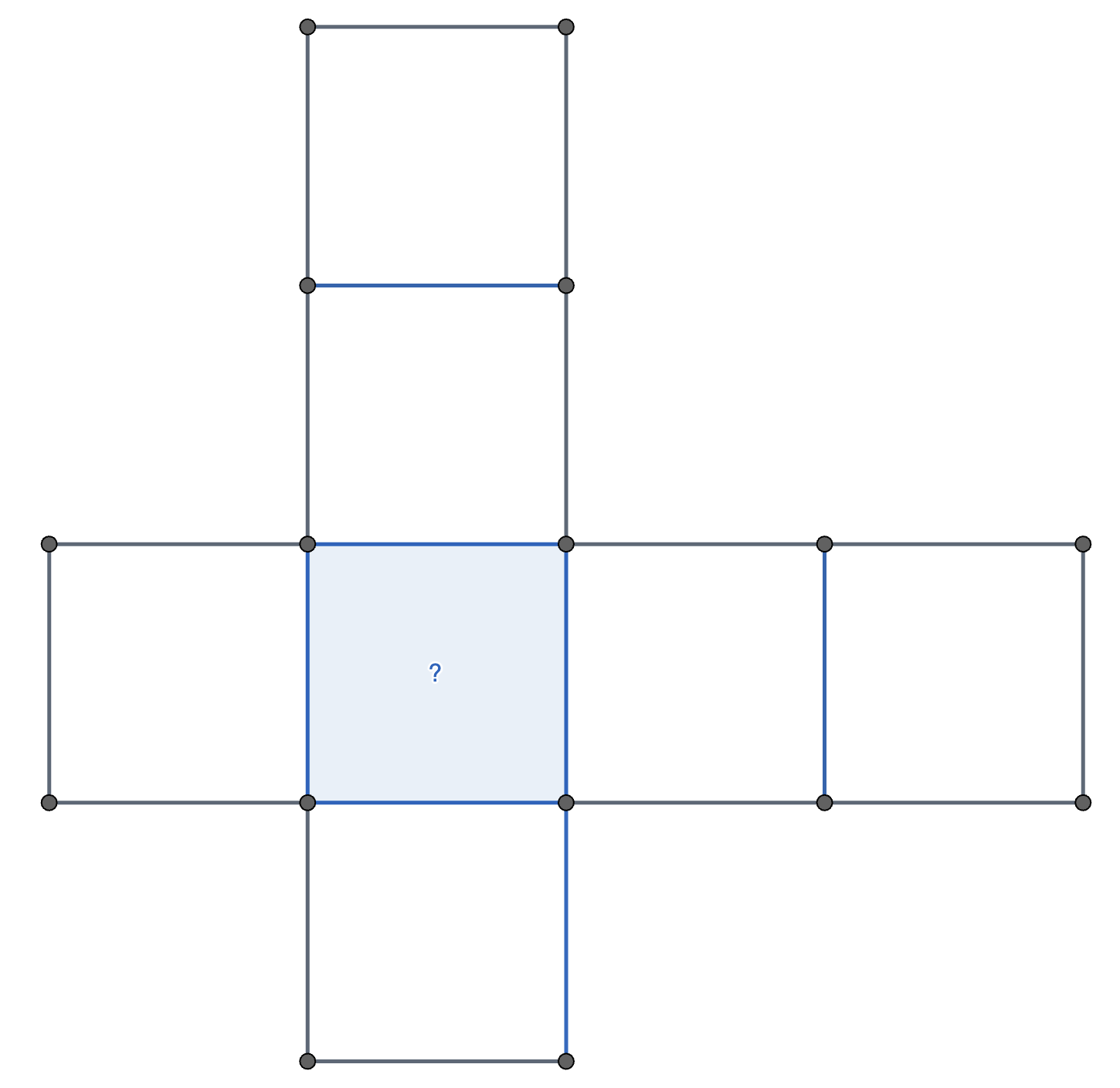
In the diagram below, I wish to write the numbers \(6, 11, 19, 23, 25, 27\) and \(29\) in the squares, but I want the sum of the numbers in the horizontal row to equal the sum of the numbers in the vertical column. What number should I put in the blue square with the question mark?

You have a row of coins and you can perform these three operations as many times as you like:

1. Remove three adjacent heads

2. Remove two adjacent tails

3. If there’s a tail followed by a heads, then turn the tail over and put a new tail after both heads

You apply these operations until you can’t make any more moves. Show that you will always get the same configuration at the end, no matter the order.

Let \(a\) be a positive integer, and let \(p\) be a prime number. Prove that \(a^p - a\) is a multiple of \(p\).

We ‘typically’ use the formula \(\frac{1}{2}bh\) for the area of a triangle, where \(b\) is the length of the base, and \(h\) is the perpendicular height. Here’s another one, called Heron’s formula.

Call the sides of the triangle \(a\), \(b\) and \(c\). The perimeter is \(a+b+c\). We call half of this the semiperimeter, \(s=\frac{a+b+c}{2}\). Then the area of this triangle is \[\sqrt{s(s-a)(s-b)(s-c)}.\] Prove this formula is correct.

There are two imposters and seven crewmates on the rocket ‘Plus’. How many ways are there for the nine people to split into three groups of three, such that each group has at least two crewmates? The two imposters and seven crewmates are all distinguishable from each other, but we’re not concerned with the order of the three groups.

For example: \(\{I_1,C_1,C_2\}\), \(\{I_2,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\) is the same as \(\{C_3,C_4,I_2\}\), \(\{C_5,C_6,C_7\}\) and \(\{I_1,C_2,C_1\}\) but different from \(\{I_2,C_1,C_2\}\), \(\{I_1,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\).

Draw the plane tiling with regular hexagons.