Problems
For all real \(x\) and \(y\), the equality \(f (x^2 + y) = f (x) + f (y^2)\) holds. Find \(f(-1)\).
It is known that \(a = x+y + \sqrt{xy}\), \(b = y + z + \sqrt{yz}\), \(c = x + z + \sqrt{xz}\). where \(x > 0\), \(y > 0\), \(z > 0\). Prove that \(a + b + \sqrt{ab} > c\).
Prove that for any odd natural number, \(a\), there exists a natural number, \(b\), such that \(2^b - 1\) is divisible by \(a\).
On a lottery ticket, it is necessary for Mary to mark 8 cells from 64. What is the probability that after the draw, in which 8 cells from 64 will also be selected (all such possibilities are equally probable), it turns out that Mary guessed
a) exactly 4 cells? b) exactly 5 cells? c) all 8 cells?
Prove that for any positive integer \(n\), it is always possible to find a number, consisting of the digits \(1\) and \(2,\) that is divisible by \(2^n\). (For example, \(2\) is divisible by \(2\), \(12\) is divisible by \(4,\) \(112\) is divisible by \(8,\) \(2112\) is divisible by \(16\) and so on...).
A sequence of natural numbers \(a_1 < a_2 < a_3 < \dots < a_n < \dots\) is such that each natural number is either a term in the sequence, can be expressed as the sum of two terms in the sequence, or perhaps the same term twice. Prove that \(a_n \leq n^2\) for any \(n=1, 2, 3,\dots\)
Out of the given numbers 1, 2, 3, ..., 1000, find the largest number \(m\) that has this property: no matter which \(m\) of these numbers you delete, among the remaining \(1000 - m\) numbers there are two, of which one is divisible by the other.
An infinite sequence of digits is given. One may consider a finite set of consecutive digits and view it as a number in decimal expression, whose digits shall be read from left to right, as usual. Prove that, for any natural number \(n\) which is relatively prime with 10, you can choose a finite set of consecutive digits which gives you a multiple of \(n\).
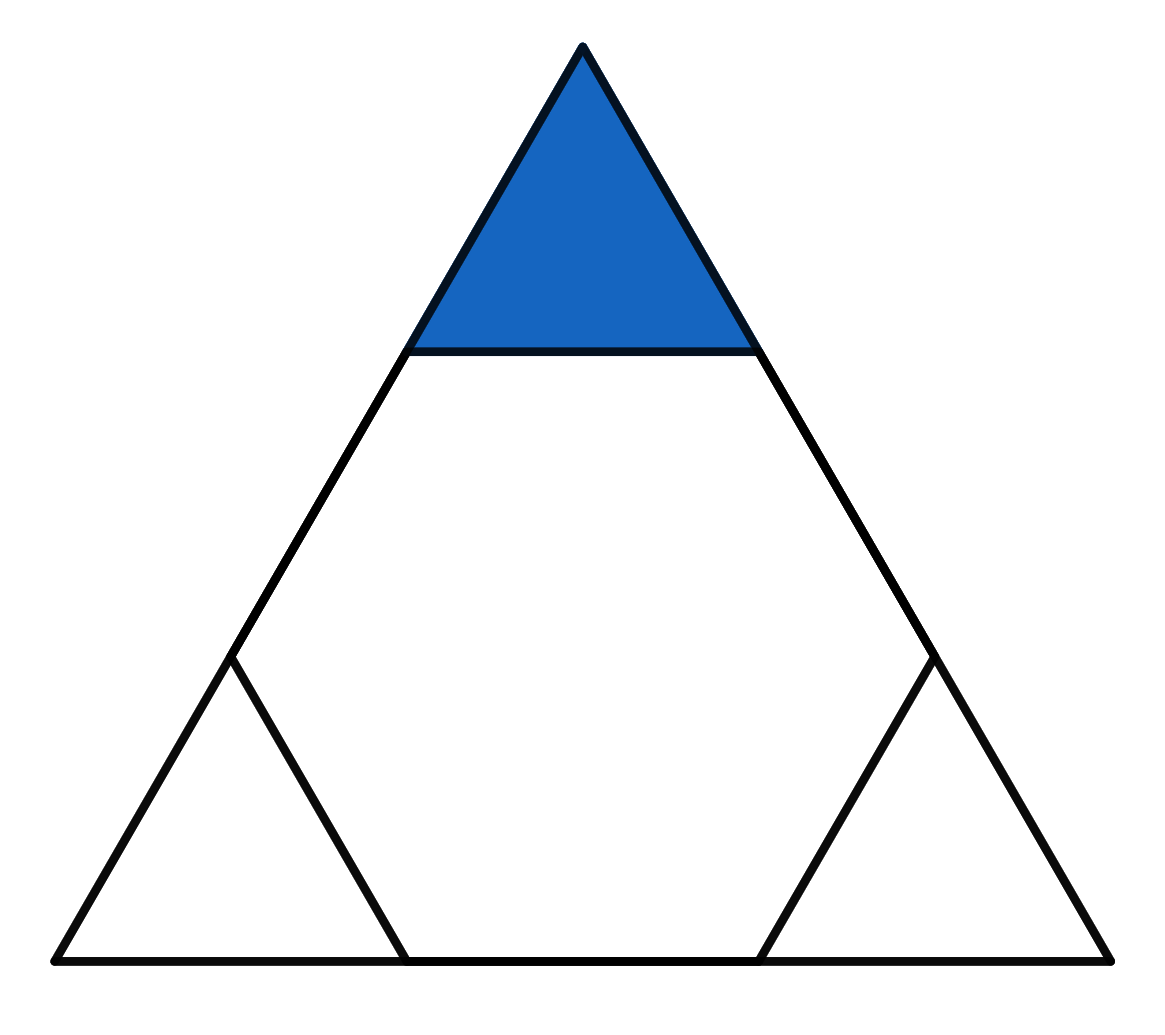
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
A quadrilateral is given; \(A\), \(B\), \(C\), \(D\) are the successive midpoints of its sides, \(P\) and \(Q\) are the midpoints of its diagonals. Prove that the triangle \(BCP\) is equal to the triangle \(ADQ\).