Problems

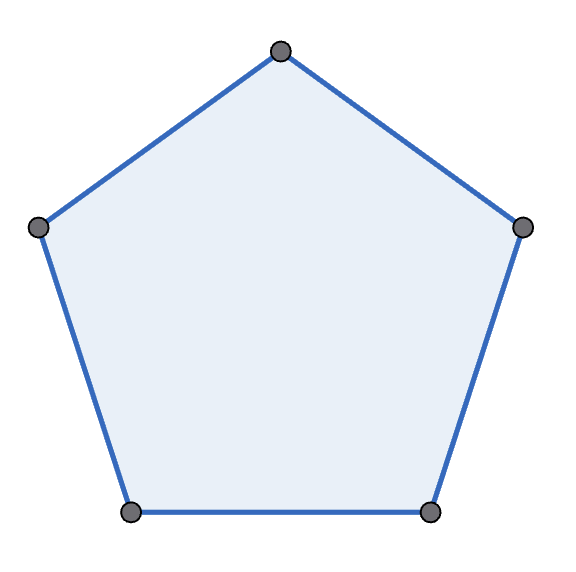
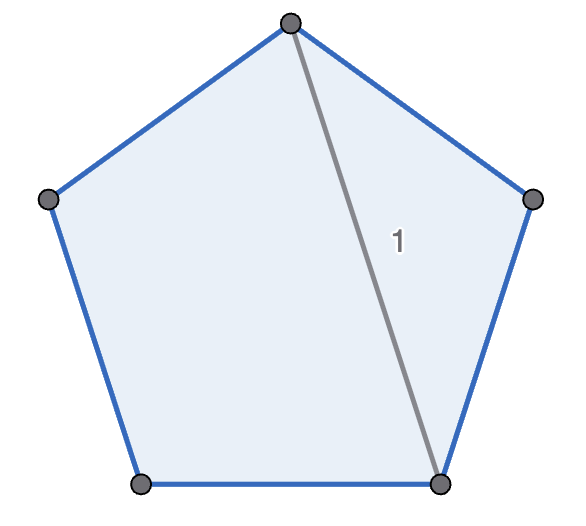
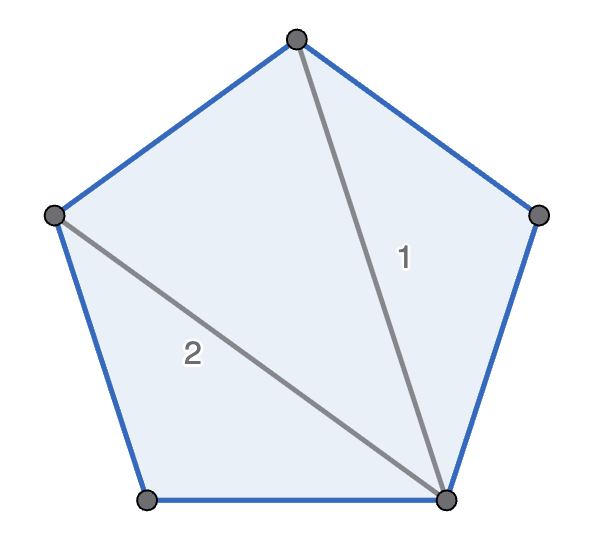
Michelle and Mondo play the following game, with Michelle going first. They start with a regular polygon, and take it in turns to move. A move is to pick two non-adjacent points in one polygon, connect them, and split that polygon into two new polygons. A player wins if their opponent cannot move - which happens if there are only triangles left. See the diagram below for an example game with a pentagon. Prove that Michelle has the winning strategy if they start with a decagon (\(10\)-sided polygon).

Let \(n\) be a positive integer. Show that \(1+3+3^2+...+3^{n-1}+3^n=\frac{3^{n+1}-1}{2}\).

Show that all integers greater than or equal to \(8\) can be written as a sum of some \(3\)s and \(5\)s. e.g. \(11=3+3+5\). Note that there’s no way to write \(7\) in such a way.

Are there any two-digit numbers which are the product of their digits?

The sum of Matt’s and Parker’s ages is \(63\) years. Matt is twice as old as Parker was when Matt was as old as Parker is now. How old are they? (Show that there’s no other ages that they could have)

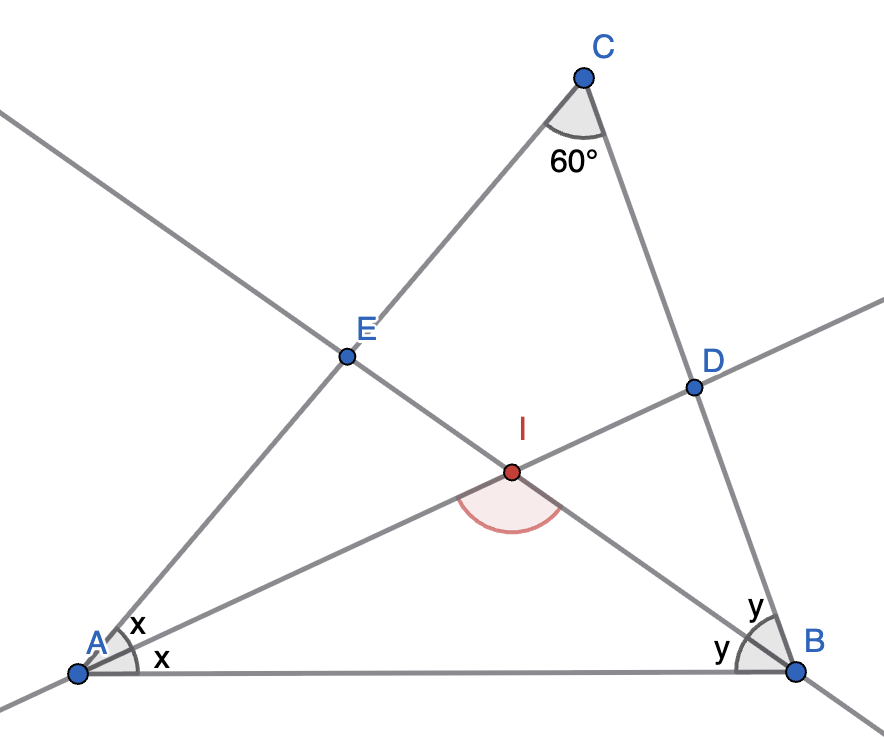
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).

Find the angle \(\angle AIB\), marked in red.

Find, with proof, all integer solutions of \(a^3+b^3=9\).

Alice and Bob were playing outdoors. A mean lady told them that at least one of them has a muddy face and everyone who has a muddy face must step forward at the same time on the count of three. Then the mean lady will leave them alone.

If a child with clean face steps forward, he is punished. If nobody steps forward, then the mean lady will do the count again. The children are not allowed to signal to each other. How can Alice and Bob avoid punishment?

Alice, Bob and Claire were playing outdoors. A mean lady told them that at least one of them has a muddy face and everyone who has a muddy face must step forward at the same time on the count of three. Then the mean lady will leave them alone.

If a child with clean face steps forward, he is punished. If nobody steps forward, then the mean lady will do the count again. The children are not allowed to signal to each other. How can Alice, Bob and Claire avoid punishment?

Alice, Bob, Claire and Daniel were playing outdoors. A mean lady told them that at least one of them has a muddy face and everyone who has a muddy face must step forward at the same time on the count of three. Then the mean lady will leave them alone.

If a child with clean face steps forward, he is punished. If nobody steps forward, then the mean lady will do the count again. The children are not allowed to signal to each other. How can Alice, Bob, Claire and Daniel avoid punishment?