Problems

Decipher the following puzzle. All the numbers indicated by the letter E, are even (not necessarily equal); all the numbers indicated by the letter O are odd (also not necessarily equal).

In a vase, there is a bouquet of 7 white and blue lilac branches. It is known that 1) at least one branch is white, 2) out of any two branches, at least one is blue. How many white branches and how many blue are there in the bouquet?

In some country there are 101 cities, and some of them are connected by roads. However, every two cities are connected by exactly one path.

How many roads are there in this country?

There are 68 coins, and it is known that any two coins differ in weight. With 100 weighings on a two-scales balance without weights, find the heaviest and lightest coin.

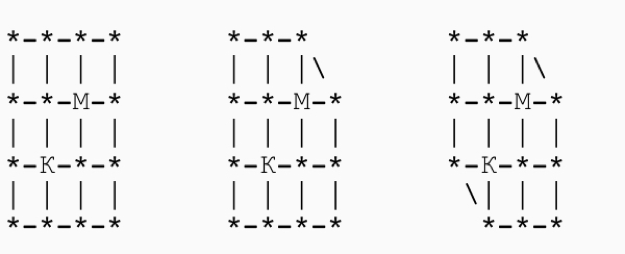
A cat tries to catch a mouse in labyrinths A, B, and C. The cat walks first, beginning with the node marked with the letter “K”. Then the mouse (from the node “M”) moves, then again the cat moves, etc. From any node the cat and mouse go to any adjacent node. If at some point the cat and mouse are in the same node, then the cat eats the mouse.

Can the cat catch the mouse in each of the cases A, B, C?

Two play a game on a chessboard \(8 \times 8\). The player who makes the first move puts a knight on the board. Then they take turns moving it (according to the usual rules), whilst you can not put the knight on a cell which he already visited. The loser is one who has nowhere to go. Who wins with the right strategy – the first player or his partner?

Two players in turn increase a natural number in such a way that at each increase the difference between the new and old values of the number is greater than zero, but less than the old value. The initial value of the number is 2. The winner is the one who can create the number 1987. Who wins with the correct strategy: the first player or his partner?

What figure should I put in place of the “?” in the number \(888 \dots 88\,?\,99 \dots 999\) (eights and nines are written 50 times each) so that it is divisible by 7?

In a certain kingdom there were 32 knights. Some of them were vassals of others (a vassal can have only one suzerain, and the suzerain is always richer than his vassal). A knight with at least four vassals is given the title of Baron. What is the largest number of barons that can exist under these conditions?

(In the kingdom the following law is enacted: “the vassal of my vassal is not my vassal”).

Sage thought of the sum of some three natural numbers, and the Patricia thought about their product.

“If I knew,” said Sage, “that your number is greater than mine, then I would immediately name the three numbers that are needed.”

“My number is smaller than yours,” Patricia answered, “and the numbers you want are ..., ... and ....”

What numbers did Patricia name?