Problems

One can hardly imagine modern life without numbers, but have you wondered when and how the numbers were invented? It turns out people started using numbers about \(42000\) years BCE supposedly to mark the dates in calendar. But how do we represent the numbers in writing? Well, there are two ways: examples of the first abstract numeral systems are generally tallying systems, the ones where the value or contribution of a digit does not depend on its position, a good example is the famous Roman numeral system: \(I\, V\, X\, L\, C\, D\, M\), here a digit has only one value: \(I\) means one, \(X\) means ten and \(C\) a hundred. However, one might struggle to express large numbers in Roman system.
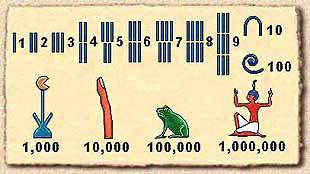
Majority of ancient civilisations, Sumerian, Egyptian, Babylonian, Chinese, Japanese, Indian used what is called positional numeral systems, where the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. All these systems, even when invented independently, have something in common, they are what is called "base-\(10\)".
Try to guess why do we use the decimal numeral system, which has exactly \(10\) digits in our everyday use. Because it does not actually have to be \(10\) digits, it could easily be \(3,8,16\), the binary system (with only digits \(0\) and \(1\)) is used in all electronic devices, since it is enough to represent any bit of information we might possibly know.

There exist various ways to prove mathematical statements, one of the possible methods, which might come handy in certain situations is called Proof by contradiction. To prove a statement we first assume that the statement is false and then deduce something that contradicts either the condition, or the assumption itself, or just common sense. Thereby concluding that the first assumption must have been wrong, so the statement is actually true.

In a lot of geometric problems the main idea is to find congruent figures. We call two polygons congruent if all their corresponding sides and angles are equal. Triangles are the easiest sort of polygons to deal with. Assume we are given two triangles \(ABC\) and \(A_1B_1C_1\) and we need to check whether they are congruent or not, some rules that help are:

• If all three corresponding sides of the triangles are equal, then the triangles are congruent.

• If, in the given triangles \(ABC\) and \(A_1B_1C_1\), two corresponding sides \(AB=A_1B_1\), \(AC=A_1C_1\) and the angles between them \(\angle BAC = \angle B_1A_1C_1\) are equal, then the triangles are congruent.

• If the sides \(AB=A_1B_1\) and pairs of the corresponding angles next to them \(\angle CAB = \angle C_1A_1B_1\) and \(\angle CBA = \angle C_1B_1A_1\) are equal, then the triangles are congruent.

At a previous geometry lesson we have derived these rules from the axioms of Euclidean geometry, so now we can just use them.

Today we will be solving problems using the Pigeonhole Principle. What is it? Simply put, suppose we are asked to put pigeons inside pigeonholes, but we have more pigeons that pigeonholes. No matter how we try to do it, there will be a pigeonhole with at least two pigeons. For example, consider the following picture, where we have \(10\) pigeons but only \(9\) pigeonholes:

No matter how hard we try to arrange the pigeons, it will be impossible to fit at most \(1\) pigeon in each pigeonhole! Here is a way to see why: suppose that in each pigeonhole there was at most \(1\) pigeon. Since we have \(9\) pigeonholes, this means we have at most \(1\times 9=9\) pigeons in total, but this is can’t be true, because we started with \(10\) pigeons!
By pigeonhole we can mean any container, and by pigeon we can mean any object that we want to place inside the containers. This is a simple but very powerful idea, and today we will learn how to use it to solve some difficult problems! Let’s start by seeing a simple example. Can you see what the pigeonholes and the pigeons should be?

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a parallelogram.

Draw a picture how Robinson used to tie the goat and the wolf in order for the goat to graze the grass in the shape of half a circle.

Draw a picture how Robinson used to tie the goat and the wolf in order for the goat to graze the grass in the shape of a young moon (see the picture below)

Draw a picture how Robinson used to tie the goat and the wolf in order for the goat to graze the grass in the shape of half a ring.

Find all the prime numbers \(p\) such that there exist natural numbers \(x\) and \(y\) for which \(p^x = y^3 + 1\).

Find all natural numbers \(n\) for which there exist integers \(a,b,c\) such that \(a+b+c = 0\) and the number \(a^n + b^n + c^n\) is prime.