Problems
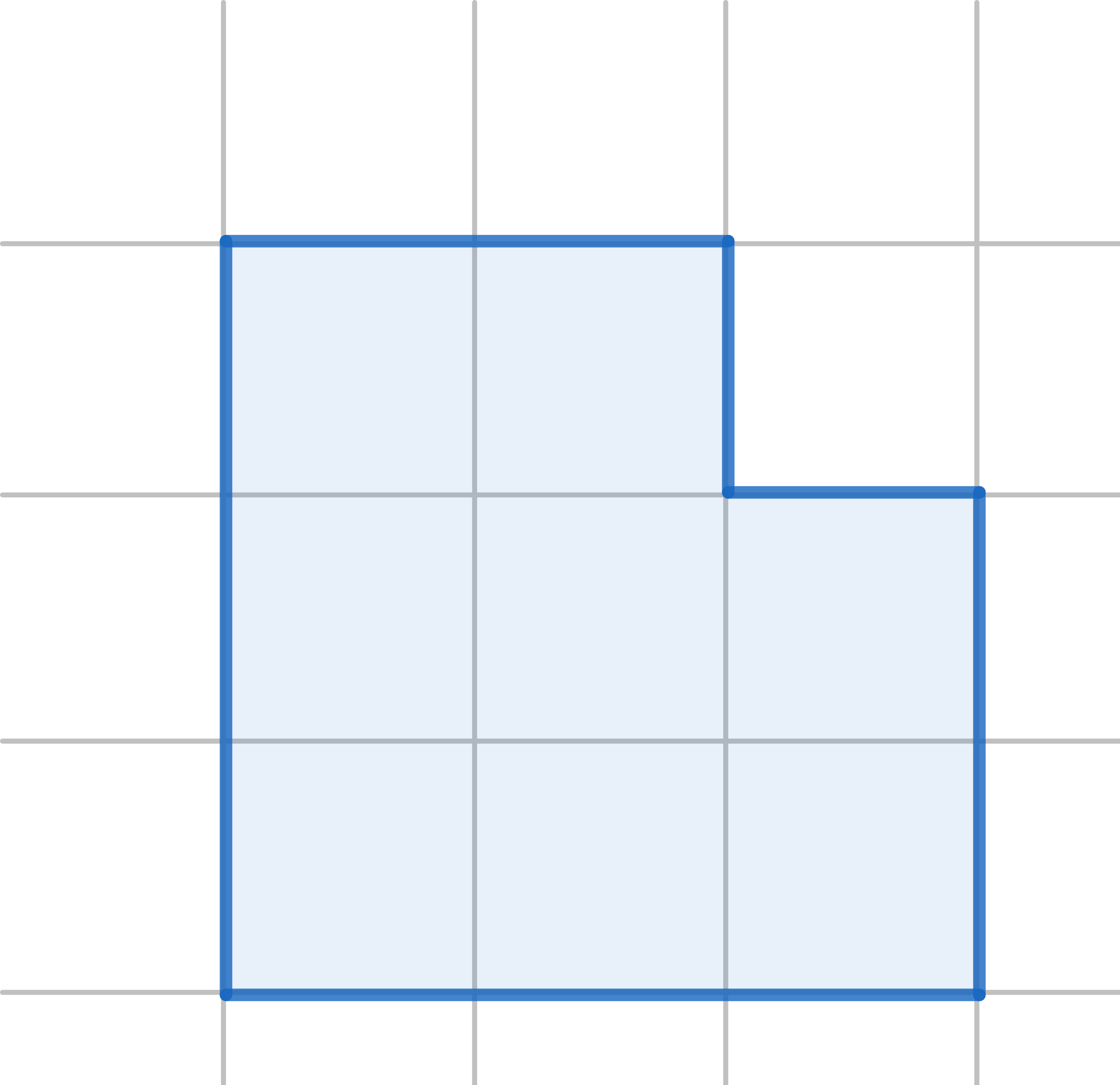
The diagram shows a \(3 \times 3\) square with one corner removed. Cut it into three pieces, not necessarily identical, which can be reassembled to make a square:
Find all possible non-zero digits \(A\) for which the following holds \((AA+AA+1) \times A = AAA\). (Recall \(AA\) means the two-digit number whose first and second digits are \(A\))
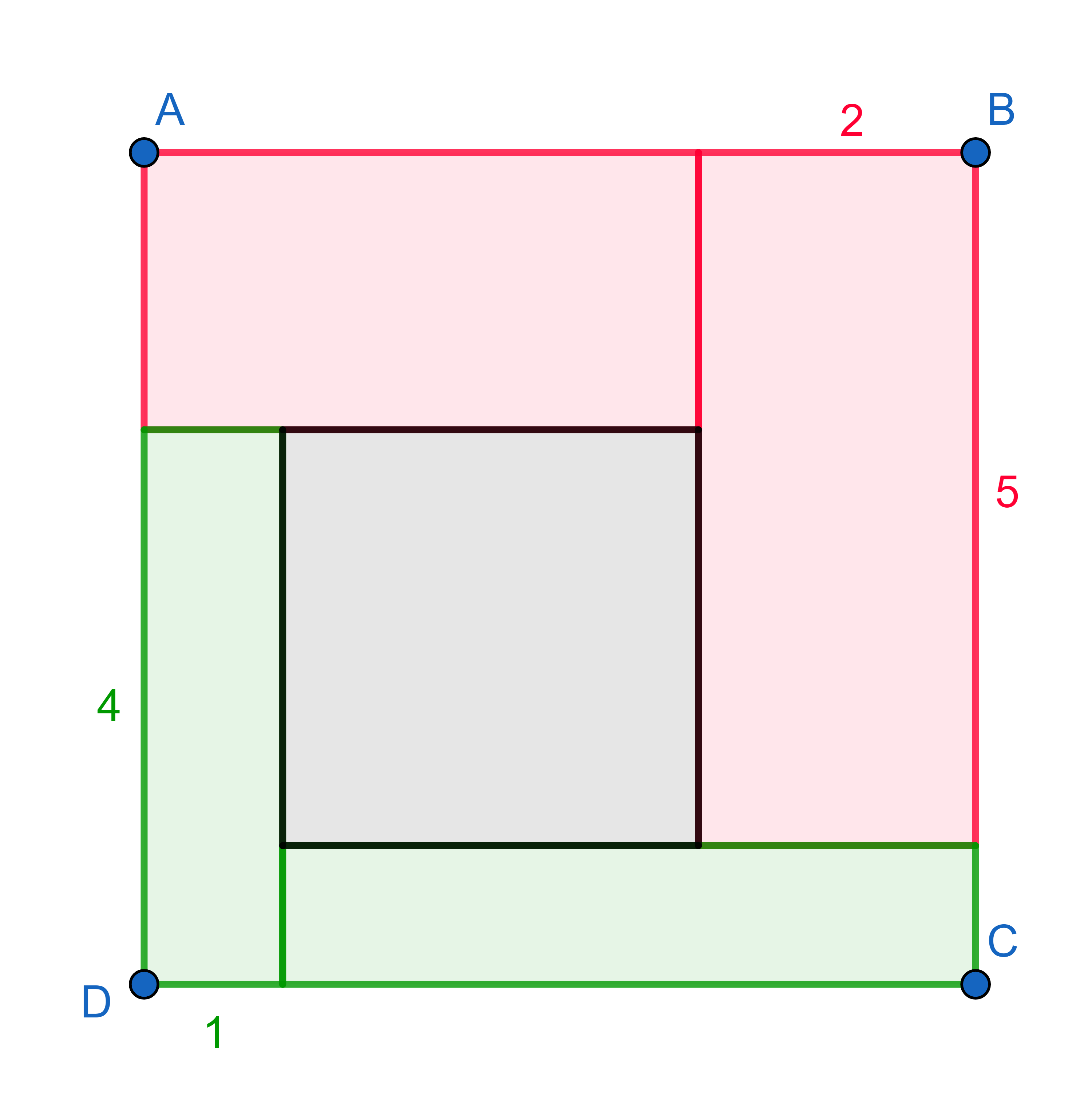
A square has been divided into \(4\) rectangles and a square. If the rectangle in the bottom left corner has dimensions \(1 \times 4\) and the one in the top right is \(2 \times 5\), what is the area of the small square in the middle?
There are \(25\) bugs sitting on the squares of a \(5 \times 5\) board, \(1\) at each square. When I clap my hands, each bug jumps to a square diagonally from where it was before. Show that after I clap my hands, at least \(5\) squares will be empty.
In a convex quadrilateral \(ABCD\), all the triangles \(\triangle ABC\), \(\triangle BCD\), \(\triangle CDA\) and \(\triangle DAB\) have equal perimeters. Show that \(ABCD\) is a rectangle.
Find the last two digits of the number \[33333333333333333347^4 - 11111111111111111147^4\]
Replace all stars with ”+” or ”\(\times\)” signs so the equation holds: \[1*2*3*4*5*6=100\] Extra brackets may be added if necessary. Please write down the expression into the answer box.
In how many ways can one change \(\pounds 2\) into coins worth \(50\)p, \(20\)p and \(10\)p? One does not necessarily need to use all available coin types, i.e. having \(5\) coins of \(20\)p and \(10\) coins of \(10\)p is allowed.
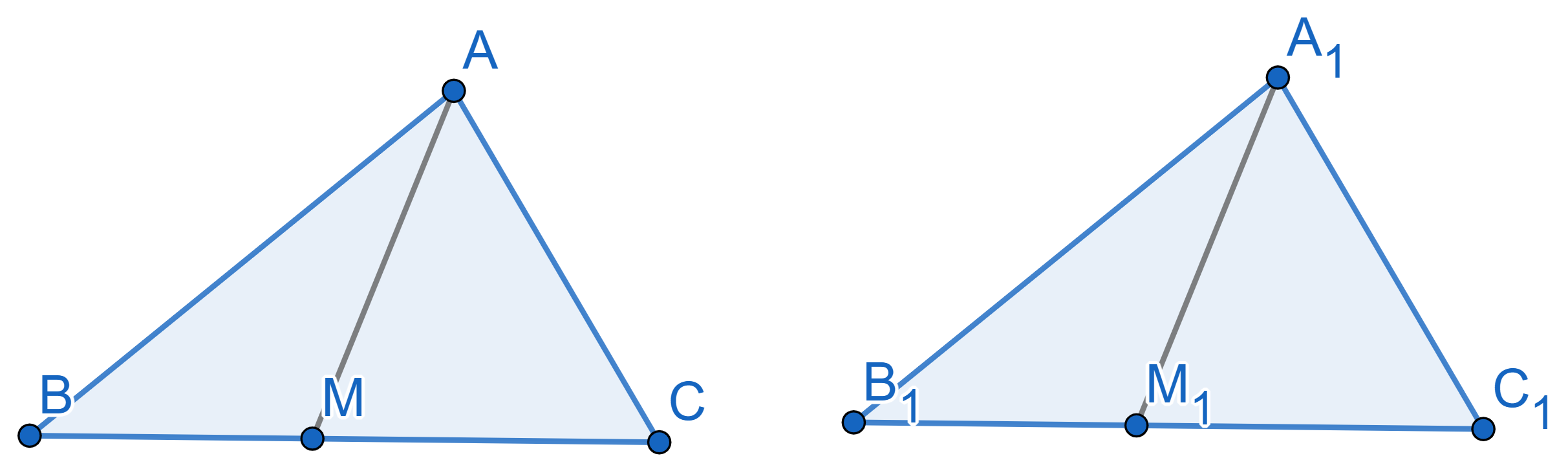
Consider two congruent triangles \(ABC\) and \(A_1B_1C_1\). We draw a point \(M\) on the side \(BC\) and a point \(M_1\) on the side \(B_1C_1\) such that the ratio of lengths
\(BM:MC\) is equal to the ratio of
lengths \(B_1M_1:M_1C_1\). Prove that
\(AM = A_1M_1\).
We call a median the segment from the vertex of a triangle to the midpoint of the opposite side. Prove that in two congruent triangles, the corresponding medians are of equal length.