Problems
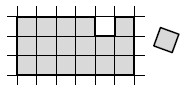
One cell was cut out of a \(3\times6\) rectangle, as seen in the diagram. How should you glue this cell in a different place to get a figure that can be cut into two identical ones? If needed, the resulting parts can be rotated and reflected.
In the sum below, different letters denote different digits and the same letters denote the same digit. \[P.Z + T.C + D.R + O.B + E.Y\] None of the five terms are integers, but the sum itself is an integer. Find the possible sums of the expression. For each possible answer, write one example with these five terms. Explain why other sums cannot be obtained.
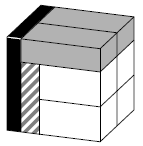
Michael made a cube with edge \(1\) out of eight bars as in the picture. All \(8\) bars have the same volume. The dimensions of the grey bars are the same as each other. Similarly, the dimensions of the white bars are the same as each other. Find the lengths of the edges of the white bars.
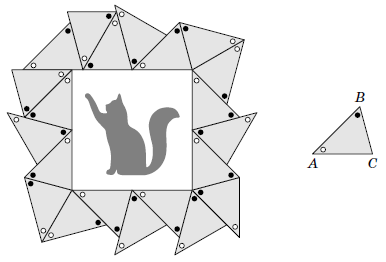
Peter went to the Museum of Modern Art and saw a square painting in a frame of an unusual shape. The frame consisted of \(21\) congruent triangles. Peter was interested in what the angles of these triangles were equal to. Help him find these angles.
Red, blue and green chameleons live on an island. One day \(35\) chameleons stood in a circle. A minute later, they all changed colour at the same time, each changing into the colour of one of their neighbours. A minute later, everyone again changed their colours at the same time into the colour of one of their neighbours. Is it ever possible that each chameleon was each of the colours red, blue and green at some point? For example, it’s allowed for a chameleon to start off blue, turn green after one minute, then turn red after the second minute. It’s not allowed for a chameleon to start off blue, turn green after one minute, but then turn back to blue after the second minute.
Let \(p\) and \(q\) be two prime numbers such that \(q = p + 2\). Prove that \(p^q + q^p\) is divisible by \(p + q\).
Let \(a\), \(b\) and \(c\) be the three side lengths of a triangle. Does there exist a triangle with side lengths \(a+1\), \(b+1\) and \(c+1\)? Does it depend on what \(a\), \(b\) and \(c\) are?
There is a triangle with side lengths \(a\), \(b\)
and \(c\). Can you form a triangle with
side lengths \(\frac{a}{b}\), \(\frac{b}{c}\) and \(\frac{c}{a}\)? Does it depend on what \(a\), \(b\)
and \(c\) are? Give a proof if it is
always possible or never possible. Otherwise, construct examples to show
the dependence on \(a\), \(b\) and \(c\).
Recall that a triangle can be drawn with side lengths \(x\), \(y\)
and \(z\) if and only if \(x+y>z\), \(y+z>x\) and \(z+x>y\).
There is a triangle with side lengths \(a\), \(b\)
and \(c\). Does there exist a triangle
with side lengths \(|a-b|\), \(|b-c|\) and \(|c-a|\)? Does it depend on what \(a\), \(b\)
and \(c\) are?
Recall that a triangle can be formed with side lengths \(x\), \(y\)
and \(z\) if and only if all the
inequalities \(x+y>z\), \(y+z>x\) and \(z+x>y\) hold.
There is a triangle with side lenghts \(a\), \(b\) and \(c\). Does there exist a triangle with sides of lengths \(a^2+bc\), \(b^2+ca\) and \(c^2+ab\)? Does it depend on the values of \(a\), \(b\) and \(c\)?