Problems
Suppose you want to compute the sum \(1+2+\dots+n\) up to some positive integer \(n\). Then you discover a curious pattern:
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \(1+2+\dots+n\) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 |
| \(\frac{n(n+1)}{2}\) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 |
We may guess at this point \(1+2+\dots+n = \frac{n(n+1)}{2}\). How can we prove it? One way is to attack the problem step by step.
When \(n=1\), the sum is just \(1\) and \(\frac{1\times(1+1)}{2}=1\). So far so good.
When \(n=2\), the sum is \(1+2 = 3\) and \(\frac{2\times(2+1)}{2}=3\). We can also see this in another way. As we already noted, \(1 = \frac{1\times(1+1)}{2}\). This means \[1+2 = \frac{1\times (1+1)}{2} + 2 = \frac{1\times2+2\times2}{2} = \frac{(1+2)\times 2}{2} = \frac{2\times(2+1)}{2}.\]
When \(n=3\), we have already proved that \(1 + 2 = \frac{2\times(2+1)}{2}\), so \[1+2+3 = \frac{2\times (2+1)}{2} + 3 = \frac{2\times3+2\times3}{2} = \frac{(2+2)\times 3}{2} = \frac{3\times(3+1)}{2}.\]
When \(n=4\), we have already proved that \(1 + 2 + 3 = \frac{3\times(3+1)}{2}\), so \[1+2+3+4 = \frac{3\times (3+1)}{2} + 4 = \frac{3\times4+2\times4}{2} = \frac{(3+2)\times 4}{2} = \frac{4\times(4+1)}{2}.\]
When \(n=5\), we have already proved that \(1 + 2 + 3 + 4 = \frac{4\times(4+1)}{2}\), so ...
It starts getting a bit boring, but hopefully you get the point. Important takeaways from the example above:
The truth of the next case depends ONLY on the previous case.
We know what we need to prove IS true for the first case, that is \(n=1\).
By repeating the same procedure starting from \(n=1\), we can eventually reach any given positive integer.
Thus, the formula is true for all positive integers (also known as natural numbers).
A diagram summarizing the idea: \[\text{true for } n=1 \implies \text{true for } n=2 \implies \text{true for } n=3 \implies \text{true for } n=4 \implies \dots\]
This is the mechanism behind induction. Formally, we can state the principle of mathematical induction as follows. Suppose we have a series of statements numbered by the positive integers: 1st statement, 2nd statement, 3rd statement and so on. Suppose that
the 1st statement is true (the base case is true);
whenever the \(n\)th statement is true, the \((n+1)\)th statement is also true (the induction step is valid assuming the induction hypothesis).
Then the statement is true for all positive integers (natural numbers). Let us revisit the example and prove it formally now using the principle of mathematical induction.
You may have seen the pigeonhole principle before, sometimes called
Dirichlet’s box principle. It says that if you have more pigeons than
pigeonholes, and you put all of the pigeons into some pigeonhole, then
there exists at least one pigeonhole with at least two pigeons. While it
sounds quite simple, it’s a powerful technique. The difficult thing is
often choosing the appropriate pigeons and pigeonholes.
It has multiple applications in various situations.
Today we will see how to use it in geometric problems.
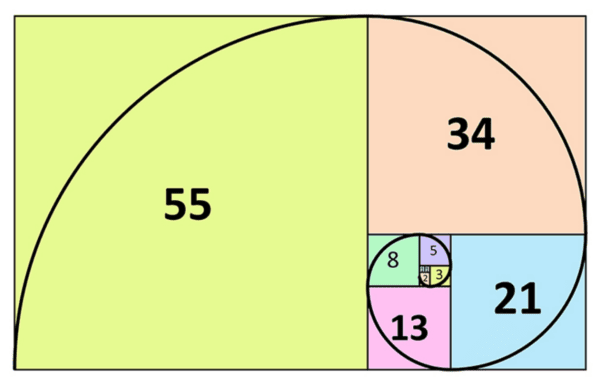
This week we’re looking at Fibonacci numbers, and other sequences of numbers.
We say that the ‘zeroth’ Fibonacci number is \(0\) and the first Fibonacci number is \(1\). Then, from that point, every Fibonacci number is found by adding the two previous Fibonacci numbers. This means that the sequence begins \(0,1,1,2,3,5,8,13,21,34,55,89,144,...\)
The Fibonacci numbers hide lots of patterns which we’ll explore today. The spiral below is formed by taking squares whose side lengths are Fibonacci numbers, and drawing quarter circles in each square.
Today we will be finding the areas of some geometric figures. Here is a brief reminder of how to calculate the area of common shapes.
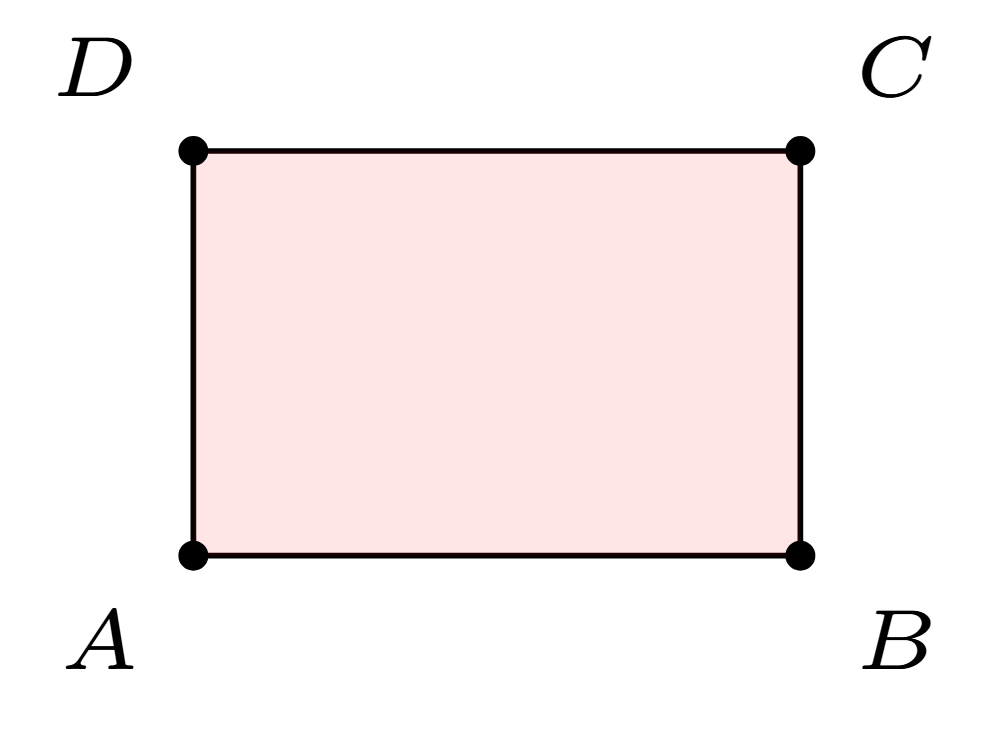
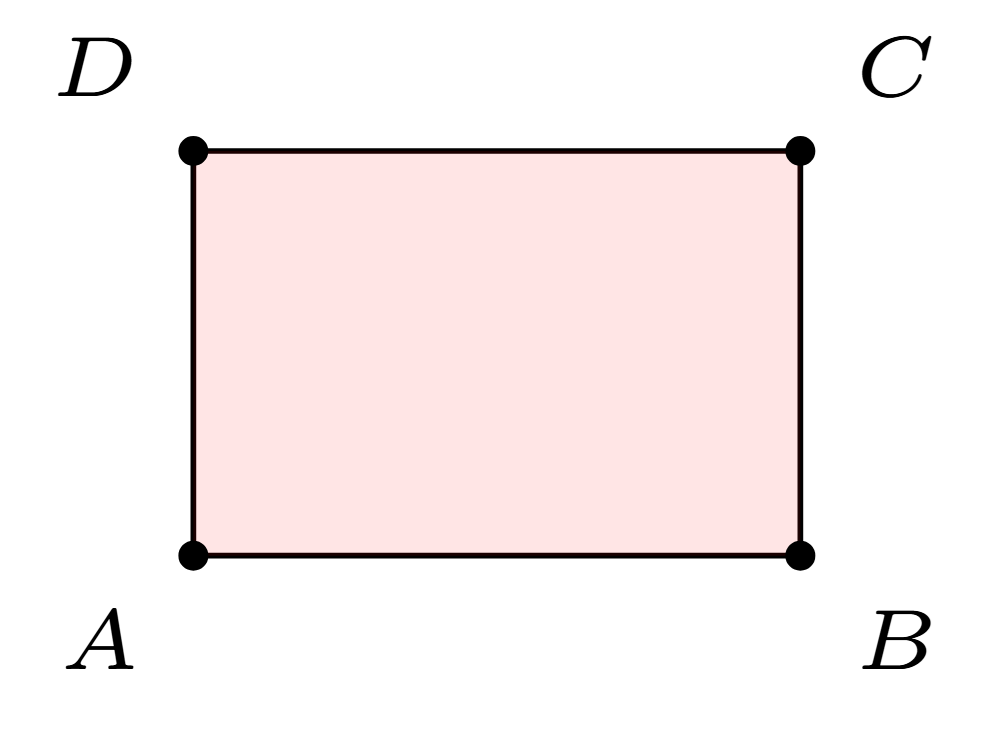
In the picture below, the area of the rectangle is \(|AB|\times |AD|\).
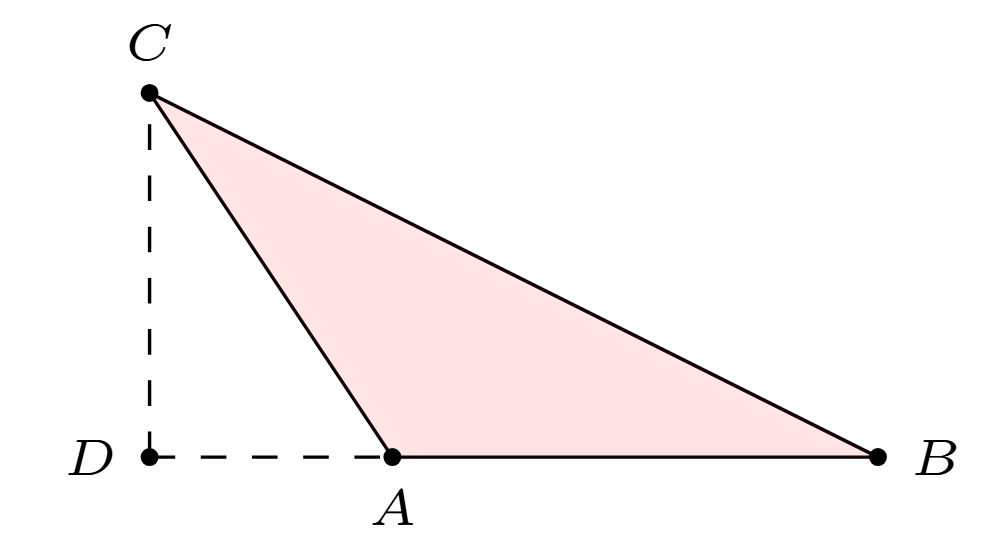
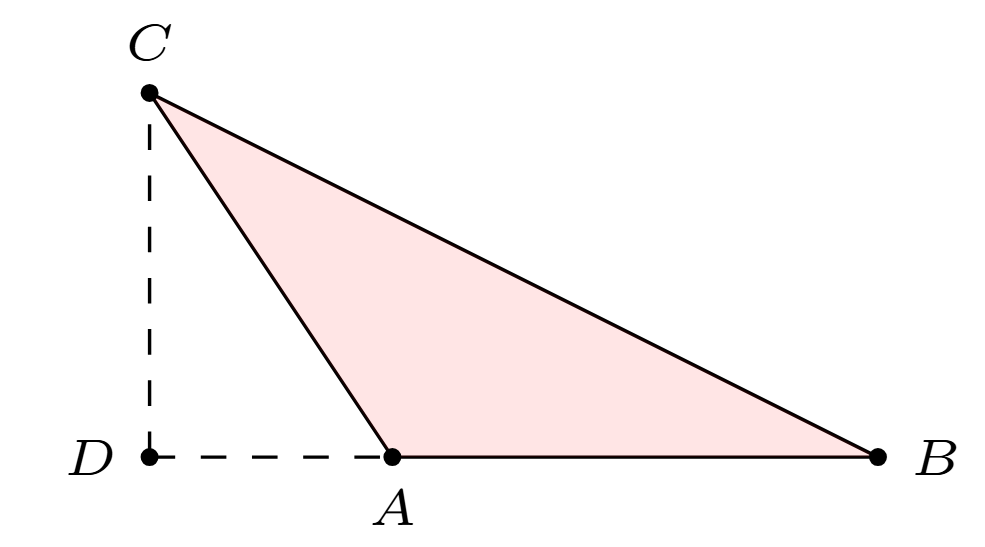
The area of a triangle is given by \(\frac{1}{2}bh\), where \(b\) is the length of a chosen base and \(h\) is the height. In this case, the segment \(AB\) is the base and \(CD\) is the altitude corresponding to the base \(AB\).
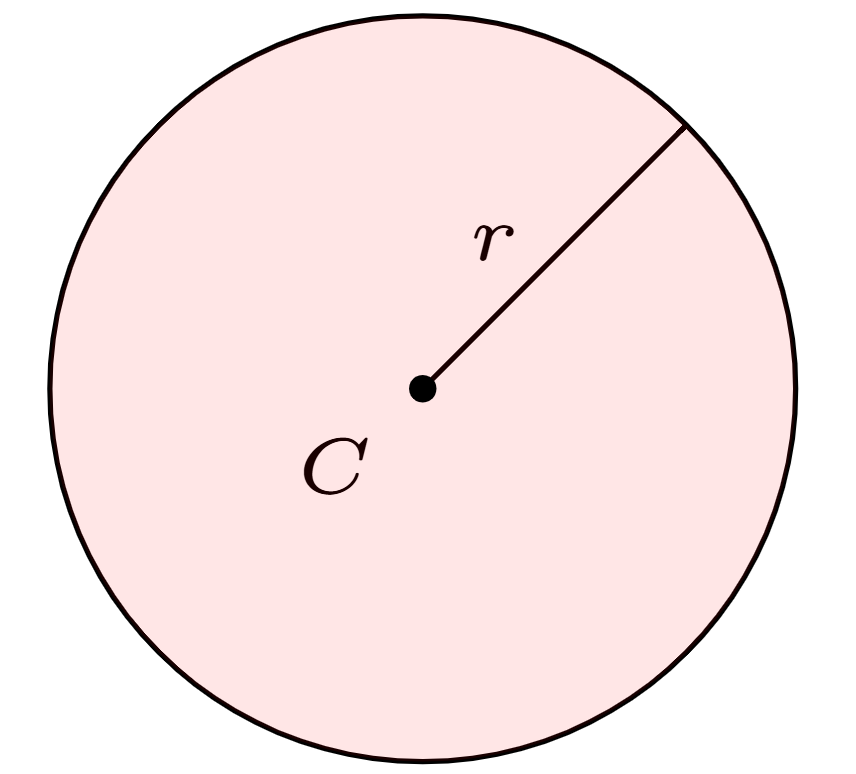
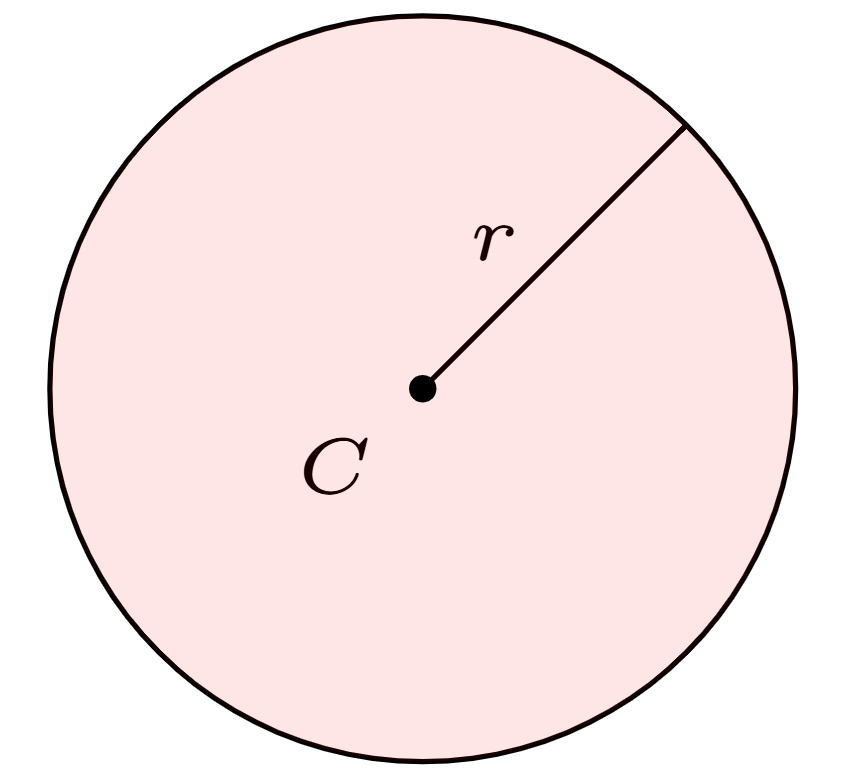
The area of a circle with radius \(r\) is \(\pi r^2\). The number \(\pi\) is approximately 3.14159 to five decimal points.
Diophantine equations are those where we’re only interested in finding the integer (whole number) solutions. Some of these equations are quite simple, while others look simple but are actually very difficult. The most famous one is Fermat’s Last Theorem, which says that when \(n>2\), there are no solutions to \[x^n+y^n=z^n.\] Pierre de Fermat claimed that he proved this in 1637, scribbling it in the margin of a book, but said “I have discovered a truly marvelous proof of this, which this margin is too narrow to contain." It was only proved by Andrew Wiles in 1995. Today’s problems won’t take 358 years to solve.
Sometimes it is hard to rigorously formulate an intuitively correct reasoning. We might not know the proper words, the proper language, we might not have the right tools. Maths problems are not an exception. When we start learning to solve them, we know nothing about possible mathematical approaches and mathematical models. Today you will learn a very useful way to visualise information: you will learn how to represent information as a graph.
A graph is a finite set of points, some of which are connected with line segments. The points of a graph are called vertices. The line segments are called edges.
In a mathematical problem, one may use vertices of a graph to represent objects in the problem, i.e. people, cities, airports, etc, and edges of the graph represent relations between the objects such as mutual friendship, railways between cities, plane routes, etc. As you will see in the examples below, representing the initial problem as a graph can considerably simplify the solution.
Today we will solve some problems about finding areas of geometric figures. You only need to know how to calculate the area of a rectangle, a triangle and a circle to be able to solve every problem in this set. Here is a brief description of the area formula for each shape.
We start with rectangles because they are easy. In the picture below, one way to find the area of the rectangle is to multiple the length of the side \(AB\) by the length of the side \(AD\).
Next we consider the area of a triangle. In general, the area of a triangle is given by \(\frac{1}{2}bh\), where \(b\) is the length of a chosen base and \(h\) is the height (the length of the altitude corresponding to that base). Finding a base and a corresponding altitude is usually straightforward. However, it can be a bit tricky if the altitude lies outside the triangle. See the picture below for one such case. The segment \(AB\) is the base and \(CD\) is the altitude.
At last, we come to the area of a circle. If a circle has radius \(r\), its area is \(\pi r^2\). A fully rigorous proof requires calculus! The number \(\pi\) is approximately 3.14159 to five decimal points.
Prime numbers are like atoms that build every integer number. That is, a prime decomposition of a number is unique and then we can use it to find the number’s factors. Today we will explore this idea a bit more.
We will introduce a couple of new terms. First, a common divisor of two numbers is simply a number that both of these numbers can be divided by. Two numbers which have no common divisors (except from 1) are called relatively prime. We can establish if two numbers are relatively prime by looking at their prime factorizations - if they share no common primes, then they cannot share a common divisor!
Out of all the common divisors two numbers have, one must be the largest. This is an important number and is called the Greatest Common Divisor (GCD). You can find it by looking at the prime factorizations of the two numbers. For every prime number appearing in both factorizations, we take the smaller power. Then we multiply all our choices together. If we divide both numbers by their GCD, the resulting numbers will have no common divisors left and so will be relatively prime.
Similar to the notion of a common divisor is the one of common multiple. It is simply a number that is divisible by both numbers. Among the common multiples, one must be the smallest – this is called the Least Common Multiple (LCM). Again, the LCM can be found by looking at the prime factorizations of the two numbers. For every prime number appearing in any of the two factorizations, we take the larger power. Then we multiply all our choices together.
A remainder is the number that is “left over" from division. Even if a number is not divisible by another number fully, we can still divide, but leaving a remainder. The remainder is less than the number we’re dividing by. For example, a remainder of \(44\) in division by \(7\) is \(2\), because \(44 = 6 \times 7 + 2\).
More generally, given any integer \(n\) and positive integer \(k\), we can always write \(n=qk+r\), where \(0\leq r<k\). We say that \(k\) goes into \(n\) \(q\) times, and a little bit (\(r\)) is left. If that little bit was larger than \(k\), it could “go into" \(n\) once more. This means we can always enforce the condition \(0\leq r<k\) on the remainder \(r\).
The general rule is that the remainder of a sum, difference or a product of two remainders is equal to the remainder of a sum, difference or a product of the original numbers. What that means is if we want to find a remainder of a product of two numbers, we need to look at the individual remainders, multiply them, and then take a remainder.
For example, \(10\) leaves the remainder \(3\) when divided by \(7\) and \(11\) leaves the remainder \(4\) when divided by \(7\). The product \(10\times11=110\) has the same remainder as the product of the individual remainders. We first multiply \(3\times4=12\) and then calculate the remainder upon division by \(7\), which is \(5\) because \(12=7+5\). That means that \(110\) gives a remainder of \(5\) when divided by \(7\). We can verify the result by calculating the remainder without simplifying first: \(110=15\times7+5\).
Here is a useful notation when discussing problems involving remainders and divisibility although it is not necessary for this problem sheet. Take two integers \(a\) and \(b\). If they differ by a multiple of a positive integer \(k\), then we write \(a \equiv b \pmod{k}\). For example, since \(24 - 10 = 2 \times 7\), we can express this fact by \(10 \equiv 24 \pmod{7}\). We say that 10 and 24 are congruent modulo 7.
Using this new notation, we can easily express the rules for remainders. Let \(a \equiv b \pmod{k}\) and \(c \equiv d \pmod{k}\). Then we have \(a + c \equiv b + d \pmod{k}\) and \(a \times c \equiv b \times d \pmod{k}\). As an example, again consider the calculation of the remainder of \(10 \times 11\) when divided by 7. We have \(10 \times 11 \equiv 3 \times 4 \equiv 12 \equiv 5 \pmod{7}\).
We make one last observation, which shows the utility of remainder when discussing divisibility. Saying that a number \(a\) is divisible by a number \(k\) is the same as saying the remainder of \(a\) when divided by \(k\) is 0. In congruence notation, the latter condition is \(a \equiv 0 \pmod{k}\).
Let’s have a look at some examples with remainders:
Today we will discover some ideas related to non-isosceles triangles. This restriction comes from the fact that in isosceles triangles, a median and a height coincide.