Problems

Suppose that \(p\) is a prime number. How many numbers are there less than \(p^2\) that are relatively prime to \(p^2\)?

How many cuboids are contained in an \(n\times n\times n\) cube? For example, we’ve got \(n^3\) cuboids of size \(1\times1\times1\), and obviously just \(1\) of size \(n\times n\times n\) (which is the whole cube itself). But we also have to count how many there of size \(1\times1\times2\), \(1\times2\times3\), and several more.

In the \(6\times7\) large rectangle shown below, how many rectangles are there in total formed by grid lines?

Simplify \(F_0-F_1+F_2-F_3+...-F_{2n-1}+F_{2n}\), where \(n\) is a positive integer.

Four different digits are given. We use each of them exactly once to construct the largest possible four-digit number. We also use each of them exactly once to construct the smallest possible four-digit number which does not start with \(0\). If the sum of these two numbers is \(10477\), what are the given digits?

On the questioners’ planet, there are two types of aliens, Cricks and Goops. These aliens can only ask questions. Cricks can only ask questions to which the answer is yes, Goops can only ask questions to which the answer is no.

There are 19 aliens standing in a circle. Each of them asks the following question “Do I have a Crick standing next to me on both sides?" Then one of them asks you in private “Is 57 a prime number?" How many Cricks were actually in the circle?

Suppose that \(n\) is a natural number and \(p\) is a prime number. How many numbers are there less than \(p^n\) that are relatively prime to \(p^n\)?

Find the minimal natural number \(n>1\) such that \(n^6 - 2n^5 - n^4 + 4n^3 - n^2 - 2n +1\) is divisible by \(2025\).

In chess, knights can move one square in one direction and two squares in a perpendicular direction. This is often seen as an ‘L’ shape on a regular chessboard. A closed knight’s tour is a path where the knight visits every square on the board exactly once, and can get to the first square from the last square.

This is a closed knight’s tour on a \(6\times6\) chessboard.

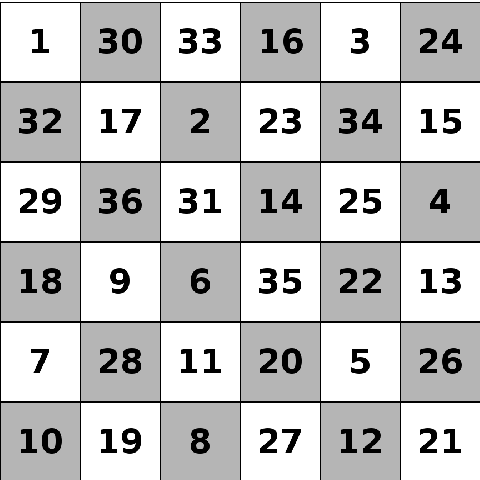
Can you draw a closed knight’s tour on a \(4\times4\) torus? That is, a \(4\times4\) square with both pairs of opposite sides identified in the same direction, like the diagram below.

Prove that one can tile the whole plane without spaces and overlaps, using any non self-intersecting quadrilaterals of the same shape. Note: quadrilaterals might not be convex.