Problems

The famous Fibonacci sequence is a sequence of numbers, which starts from two ones, and then each consecutive term is a sum of the previous two. It describes many things in nature. In a symbolic form we can write: \(F_0 = 1, F_1 = 1, F_n = F_{n-1} + F_{n-2}\).
Show that \[F_0+F_1+ F_2 + \dots + F_n = F_{n+2}-1\]

In a certain country, there are \(n\) cities. Some of them are connected by roads, all of which go in both directions. It is possible to get from any city to any other city using only roads. However, for any pair of cities, there is always only one way to get from one of them to the other and there are no alternative routes.
Show that there are exactly \(n-1\) roads in this country.

If \(x\) is any positive real number and \(n \ge 2\) is a natural number, show that \[(1+x)^n > 1+nx\]

Anna and Bob play a game with the following rules: they both receive a positive integer number. They do not know each other’s numbers, but they do know that their numbers come one after another – they do not know which one is larger. (If Anna gets \(n\), Bob gets either \(n-1\) or \(n+1\)). Anna then asks Bob – “do you know what number I have?” If Bob does know, he has to say Anna’s number and he wins the game. If he does not, he has to say that he does not. Then, he asks Anna if she knows his number. If Anna does not know, she asks Bob. This continues until one of them finds out what is the other’s number. Assuming that both Anna and Bob know mathematics sufficiently well to be able to solve this problem, find out who wins the game and how.
For simplicity let’s assume Bob always gets the odd number and Anna always gets the even number - two consecutive numbers have opposite parity!

A real number \(y\) is such that \(y+\frac1{y}\) happens to be an integer. Show that for any natural \(n\), it is also true that \(y^n + \frac1{y^n}\) is an integer.

Show how to cover the plane with triangles of the following shape.

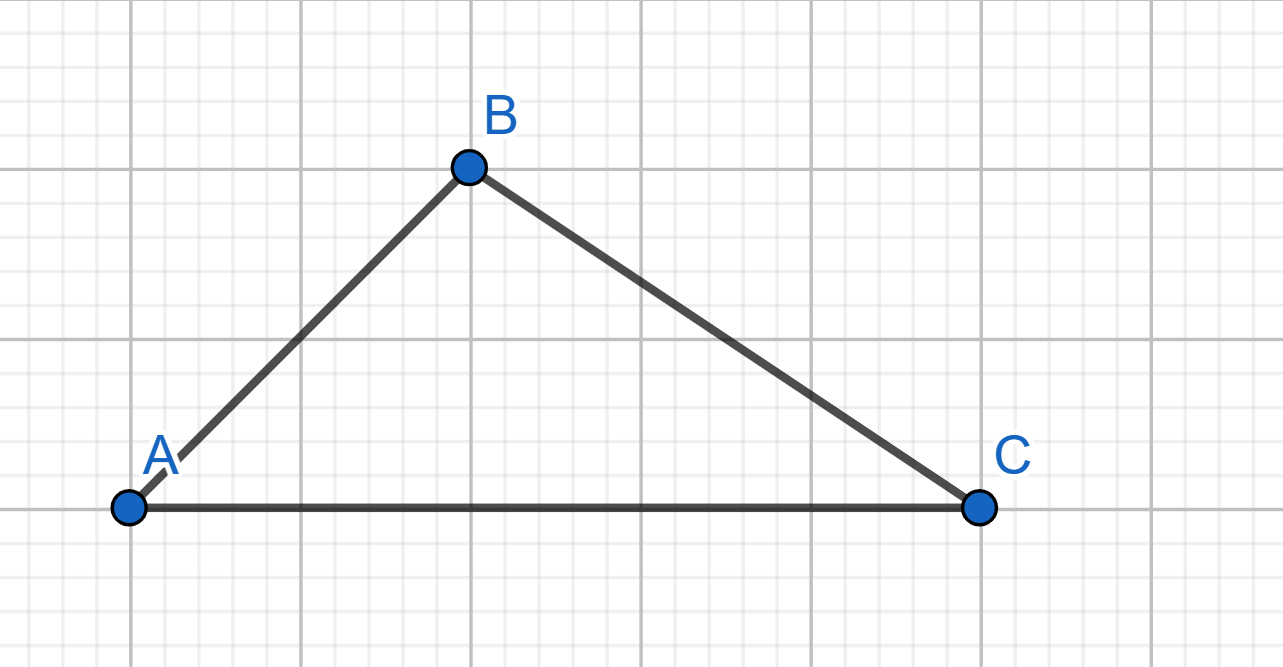
Draw how to tile the whole plane with figures, made from squares \(1\times 1\), \(2\times 2\), \(3\times 3\), and \(4\times 4\), where squares are used the same amount of times in the design of the figure.

Show how to cover the plane with convex quadrilaterals.

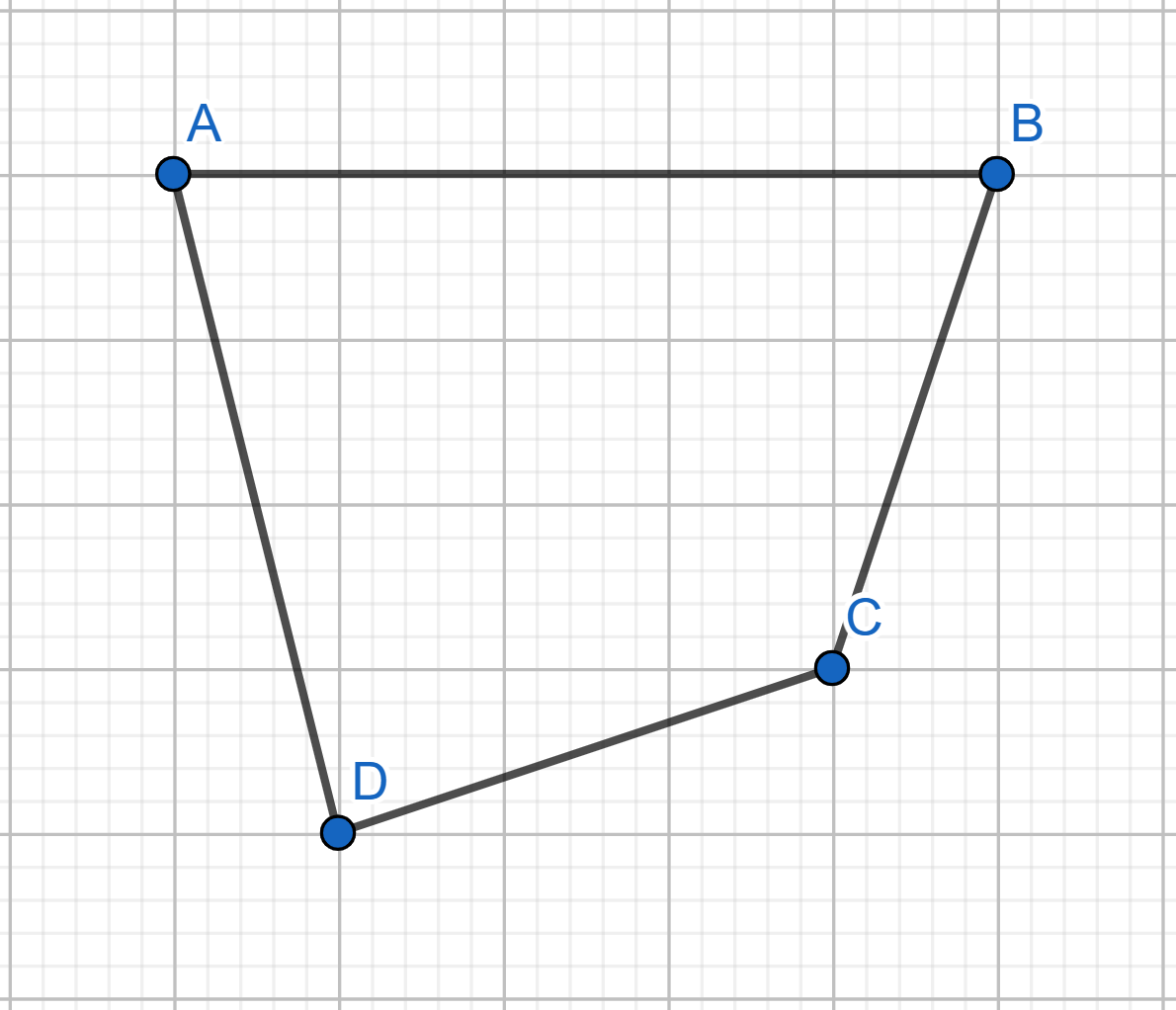
Draw the plane tiling with:

• squares;

• rectangles \(1\times 3\);

• regular triangles;

• regular hexagons.

Draw the plane tiling using trapeziums of the following shape:

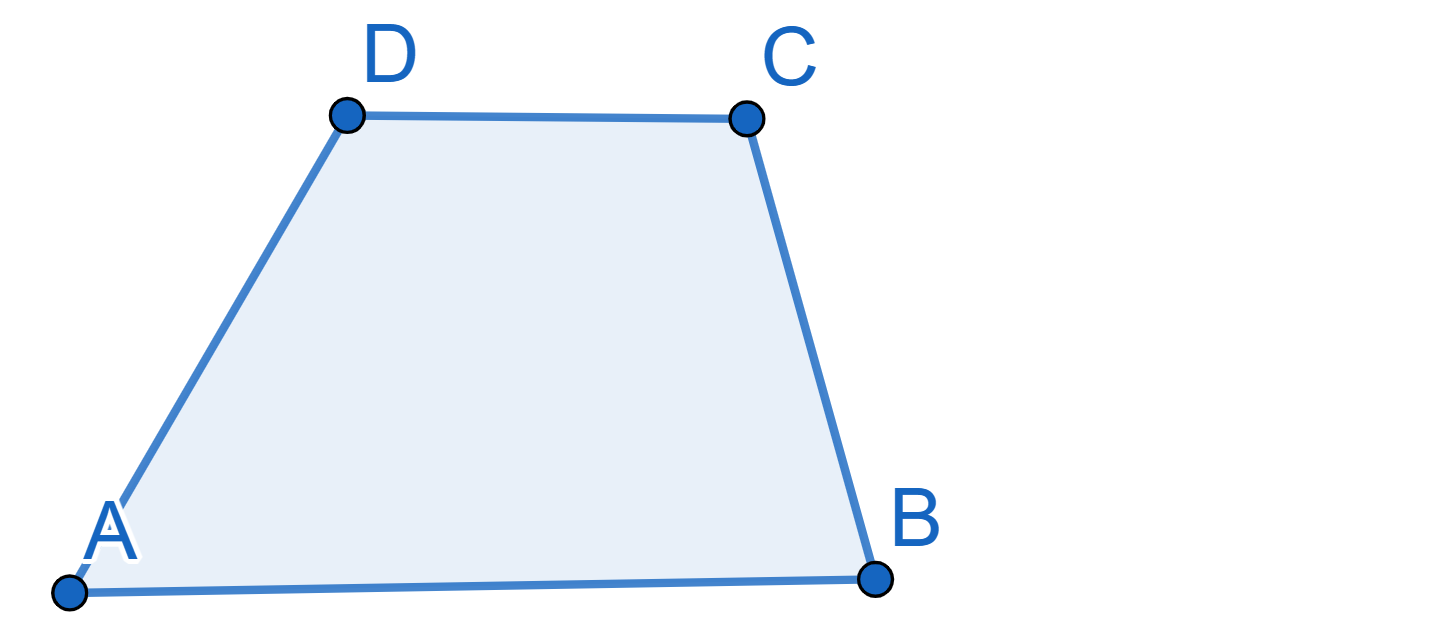
Here the sides \(AB\) and \(CD\) are parallel.