Problems

Some Star Trek fans and some Doctor Who fans met at a science fiction convention. It turned out that everyone knew exactly three people at the convention. However, none of the Star Trek fans knew each other and none of the Doctor Who fans knew each other. Show that there are the same number of Star Trek fans as the number of Doctor Who fans at the convention.

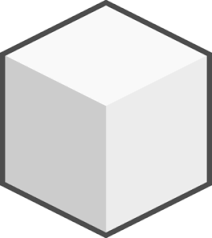
Starting at one of the vertices, an ant wishes to walk each of the \(12\) edges of a sugar cube exactly once. Prove that this is impossible.

Noah has \(10\) dogs, who he wishes to group into \(5\) pairs for \(5\) families, each of whom want two dogs. However, the dogs are quite picky, and can’t be paired with most of the other dogs. None in the first group will go with each other: an alsatian, a border collie, a chihuahua, a dachshund and an English bulldog. None in the second group will go with each other: a foxhound, a greyhound, a harrier, an Irish setter and a Jack Russell. Furthermore,
The alsatian is the least picky and can be paired with any in the second group.

The border collie won’t go with the foxhound, but will go with any other dog in the second group.

The chihuahua and the dachshund will only go with the Irish setter and the Jack Russell.

Additionally, none of the foxhound, greyhound and harrier will go with the English bulldog.
Is it possible to pair up the \(10\) dogs?

Multiply an odd number by the two numbers either side of it. Prove that the final product is divisible by \(24\).

Mattia is thinking of a big positive integer. He tells you what this number to the power of \(4\) is. Unfortunately it’s so large that you tune out, and only hear that the final digit is \(4\). How do you know that he’s lying?

You might want to know what day of the week your birthday is this year. Mathematician John Conway invented an algorithm called the ‘Doomsday Rule’ to determine which day of the week a particular date falls on. It works by finding the ‘anchor day’ for the year that you’re working in. For \(2025\), the anchor day is Friday. Certain days in the calendar always fall on the anchor day. Some memorable ones are the following:
‘\(0\)’ of March - which is \(29\)th February in a leap year, and \(28\)th February otherwise.

\(4\)th April, \(6\)th June, \(8\)th August, \(10\)th October and \(12\)th December. These are easier to remember as \(4/4\), \(6/6\), \(8/8\), \(10/10\) and \(12/12\).

\(9\)th May, \(11\)th July, \(5\)th September and \(7\)th November. These are easier to see as \(9/5\), \(11/7\), \(5/9\) and \(7/11\). A mnemonic for them is “9-5 at the 7-11".
Then find the nearest one of these dates to the date that you’re looking for and find remainders.

For example, \(\pi\) day, (\(14\)th March, which is written \(3/14\) in American date notation. It’s also Albert Einstein’s birthday) is exactly \(14\) days after ‘\(0\)’th March, so is the same day of the week - Friday in \(2025\).

What day of the week will \(25\)th December be in \(2025\)?

\(6\) friends get together for a game of three versus three basketball. In how many ways can they be split into two teams? The order of the two teams doesn’t matter, and the order within the teams doesn’t matter.

That is, we count A,B,C vs. D,E,F as the same splitting as F,D,E vs A,C,B.

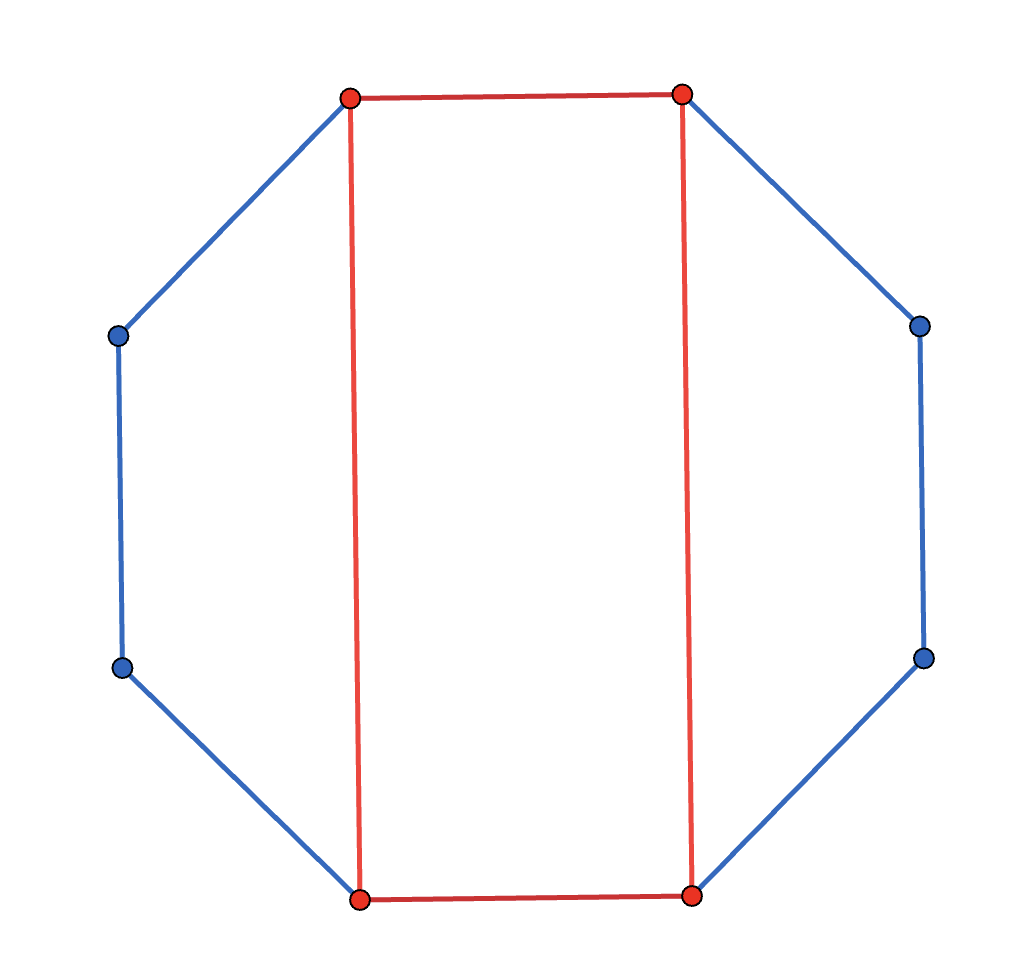
Below is a regular octagon. Given that its side length is \(1\), what’s the difference between the area of the red rectangle and the rest of the octagon?

\(x\), \(y\) and \(z\) are all integers. We’re told that \[\begin{align} x^3yz&=6\\ xy^3z&=24\\ xyz^3&=54. \end{align}\] What’s \(xyz\)?

In the diagram, all the small squares are of the same size. What fraction of the large square is shaded?