Problems

Place eight independent queens on a standard \(8\times8\) chessboard.

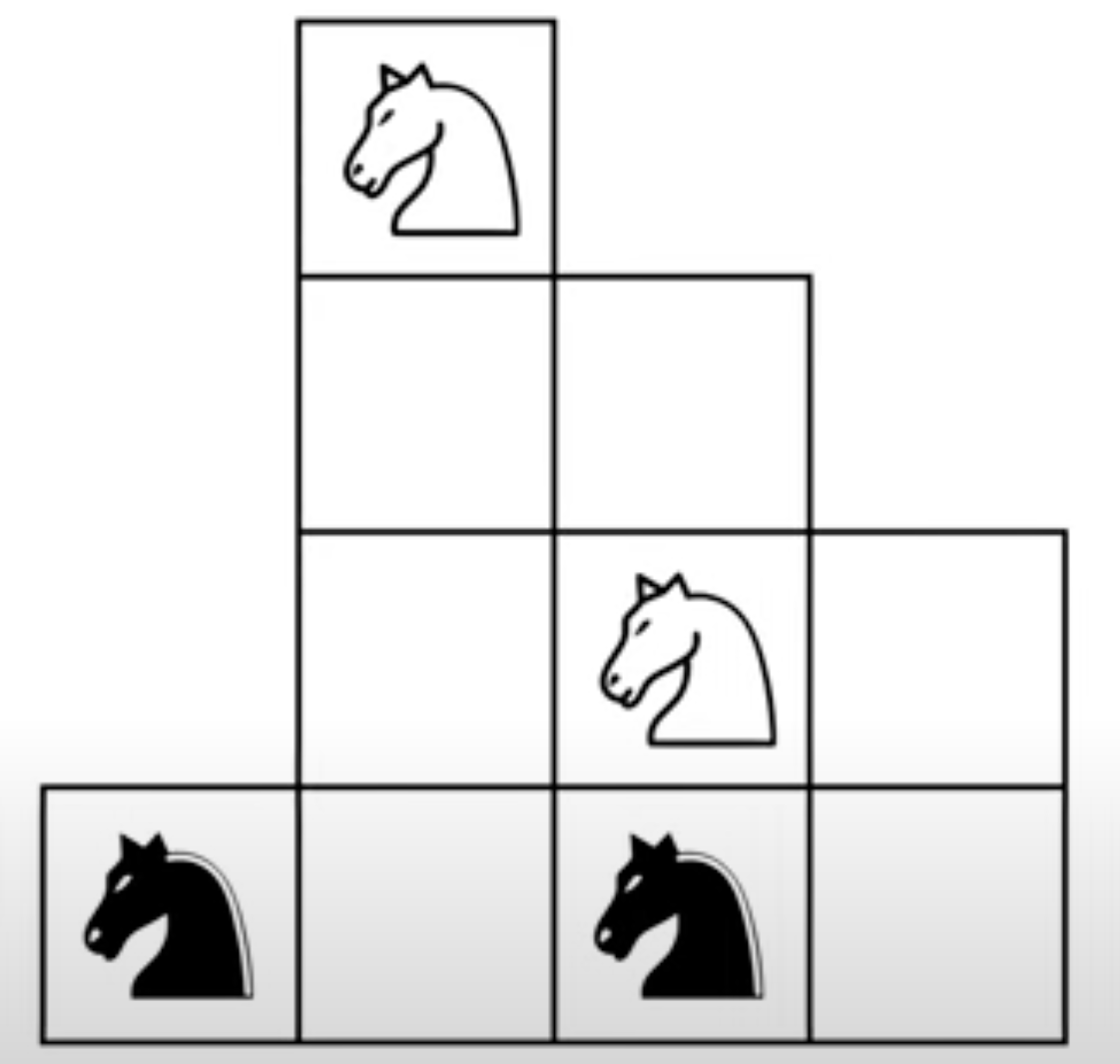
Show how to swap the two pairs of knights on the following strangely-shaped grid. That is, the knights make one move at a time, and you’re trying to get the black nights to where the white knights are, and the white knights to where the black knights are.

Let \(n\) be a positive integer. Prove that it’s impossible to have a closed knight’s tour on a \(4\times n\) grid.

Find an open knight’s tour on a \(2\times2\times2\) cube.

Let \(s\) and \(t\) be two positive integers. Can we have \(s^2=t^2+2\)?

Four football teams play in a tournament. There’s the Ulams (\(U\)), the Vandermondes (\(V\)), the Wittgensteins (\(W\)) and the Xenos (\(X\)). Each team plays every other team exactly once, and matches can end in a draw.
If a game ends in a draw, then both teams get \(1\) point. Otherwise, the winning team gets \(3\) points and the losing team gets \(0\) points. At the end of the tournament, the teams have the following points totals: \(U\) has \(7\), \(V\) has \(4\), \(W\) has \(3\) and \(X\) has \(2\).

Work out the results of each match, including showing that there’s no other way the results could have played out.

Naomi and Rory get tired of playing Nim, so decide to change the rules to mix it up. They call their new variant ‘Wonim’. There are two piles of four matchsticks each. They take it in turns to take matchsticks. Each player has to take at least one matchstick, and they can take as many as they like from one pile only.

Except, their new rule is that a player cannot take the same number of matchsticks that their opponent just did. For example, consider Wonim(\(5\),\(10\)). If Naomi’s first move is to take \(4\) matchsticks from the pile of size \(5\), turning the game to Wonim(\(1\),\(10\)), then Rory cannot take \(4\) matchsticks - he has to take more or less. A player loses if they cannot go - this can happen if there are no matchsticks left, or if there are matchsticks left, but they can’t take any since their opponent took that number. e.g. Wonim(\(1\),\(1\)), Naomi takes \(1\), Rory faces Wonim(\(1\)) but can’t move since he’s not allowed to take \(1\).

In the game Wonim(\(4\),\(4\)) with Naomi going first, who has the winning strategy?

Imagine a \(5\times6\) rectangular chocolate bar, and you want to split it between you and your \(29\) closest friends, so that each person gets one square. You repeatedly snap the chocolate bar along the grid lines until the rectangle is in \(30\) individual squares. You can’t snap more than one rectangle at a time.

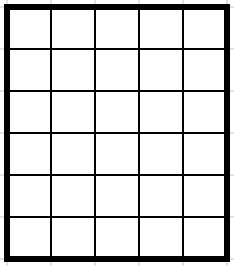
The diagram shows a couple of choices for your first two snaps. For example, in the first picture, you snap along a vertical line, and then snap the left rectangle along a horizontal line.
How many snaps do you need to get the \(30\) squares?

Prove that it’s impossible to cover a \(4\times9\) rectangle with \(9\) ‘T’ tetrominoes (one copy seen in red).

Prove that \(n^{n+1}>(n+1)^n\) for integers \(n\ge3\).