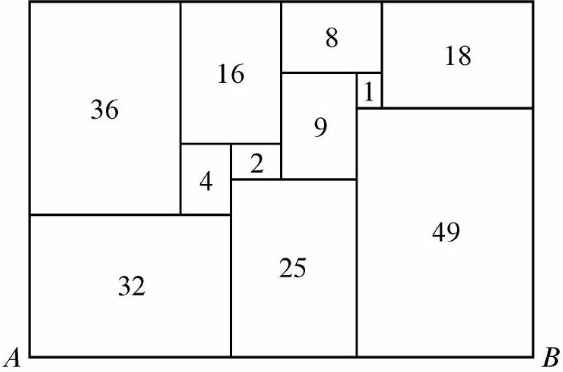
Problems
There are six symmetries of an equilateral triangle: three reflections, and three rotations (thinking of the identity as one the rotations). Label the three reflections \(s_1\), \(s_2\) and \(s_3\). Label the identity by \(e\), rotation by \(120^{\circ}\) as \(r_1\), and rotation by \(240^{\circ}\) clockwise as \(r_2\).
Note the following definition: Each symmetry has an inverse. Suppose we apply symmetry \(x\). Then there is some symmetry we can apply after \(x\), which means that overall, we’ve applied the identity. What are the inverses of \(r_1\) and \(s_1\)?
Think about the symmetries of an equilateral triangle. Is applying rotation by \(120^{\circ}\), and then reflecting in the vertical median the same as applying these two symmetries the other way around?
Let \(n\ge3\) be a positive integer. A regular \(n\)-gon is a polygon with \(n\) sides where every side has the same length, and every angle is the same. For example, a regular \(3\)-gon is an equilateral triangle, and a regular \(4\)-gon is a square.
What symmetries does a regular \(n\)-gon have, and how many?
The set of symmetries of an object (e.g. a square) form an object called a group. We can formally define a group \(G\) as follows.
A is a non-empty set \(G\) with a binary operation \(*\) satisfying the following axioms (you can think of them as rules). A binary operation takes two elements of \(G\) and gives another element of \(G\).
Closure: For all \(g\) and \(h\) in \(G\), \(g*h\) is also in \(G\).
Identity: There is an element \(e\) of \(G\) such that \(e*g=g=g*e\) for all \(g\) in \(G\).
Associativity: For all \(g\), \(h\) and \(k\) in \(G\), \((g*h)*k=g*(h*k)\).
Inverses: For every \(g\) in \(G\), there exists a \(g^{-1}\) in \(G\) such that \(g*g^{-1}=e\).
Prove that the symmetries of the ‘reduce-reuse-recycle’ symbol form a group.

Take a pile of cards, Ace to 7 of Diamonds. Consider the following shuffle: simultaneously move the first card to the third position, the third card to the fifth position, the fifth card to the seventh position, and the seventh card to the first position. Also move the second card to the fourth position, the fourth card to the sixth position and the sixth card to the second position.
How many times do you have to do this one specific shuffle in a row to get back to where you started?
How many permutations are there of 4 cards leaving no card in the same position as before?
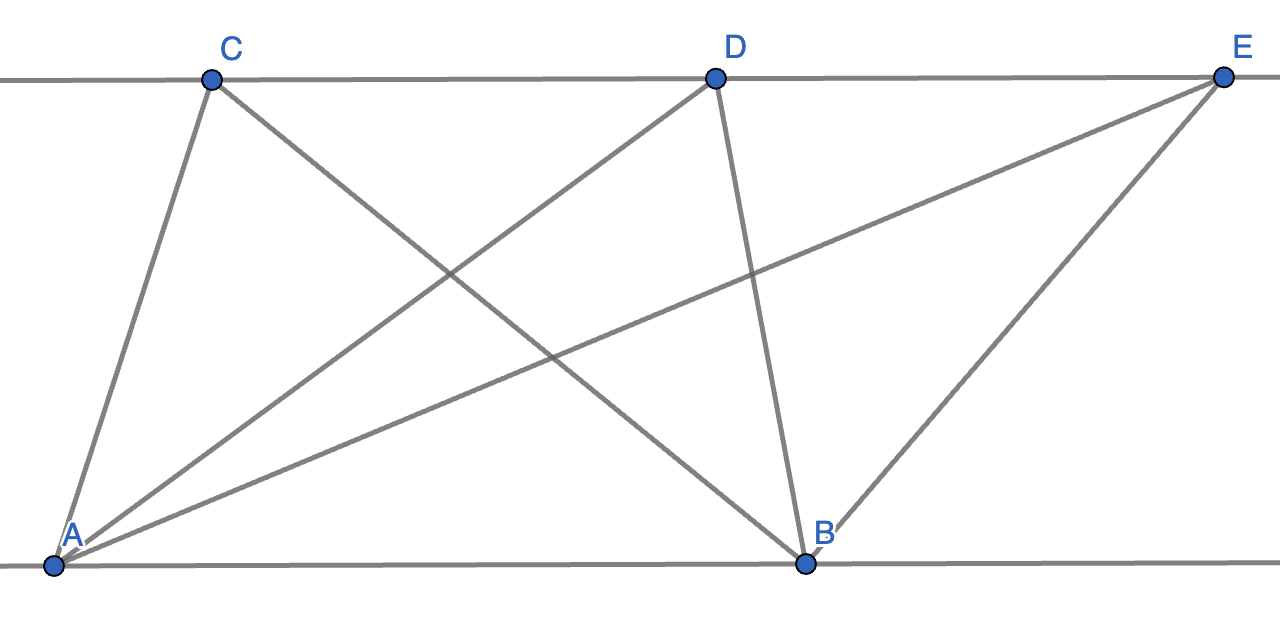
Lines \(AB\) and \(CDE\) are parallel. Which triangle out of \(\triangle ABC\), \(\triangle ABD\) and \(\triangle ABE\) has the greatest area?
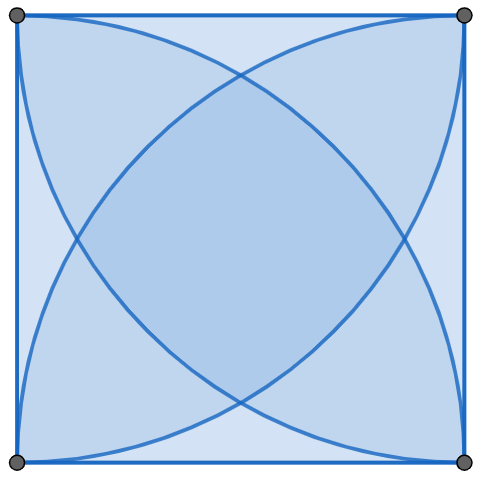
We have a square of side length 1. At each vertex of the square, we draw a circle of radius 1. What is the area bounded by all four circles?
A simple polygon is a polygon that does not intersect itself and has no holes. Suppose we have a simple polygon \(S\) whose vertices consists of only integer coordinates.
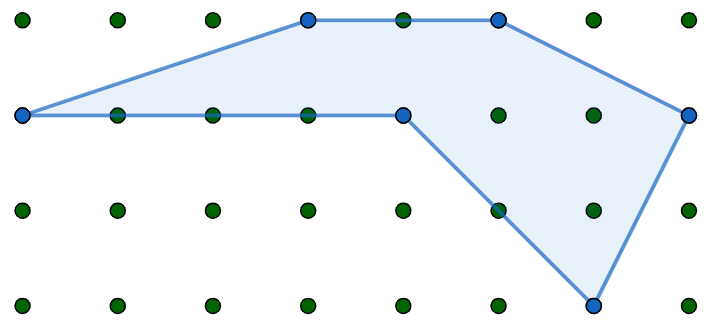
The area turns out to be remarkably easy to calculate. Count up the number of points with integer coordinate inside the polygon and on the boundary; call them \(i\) and \(b\) respectively. The area is then \[A(S) = i+\frac{b}{2}-1.\]
In the picture above, \(i=3\) and \(b=11\), so \(A(S) = \frac{15}{2}\). Prove that this formula for the area \(A(S)\) is correct.