Problems

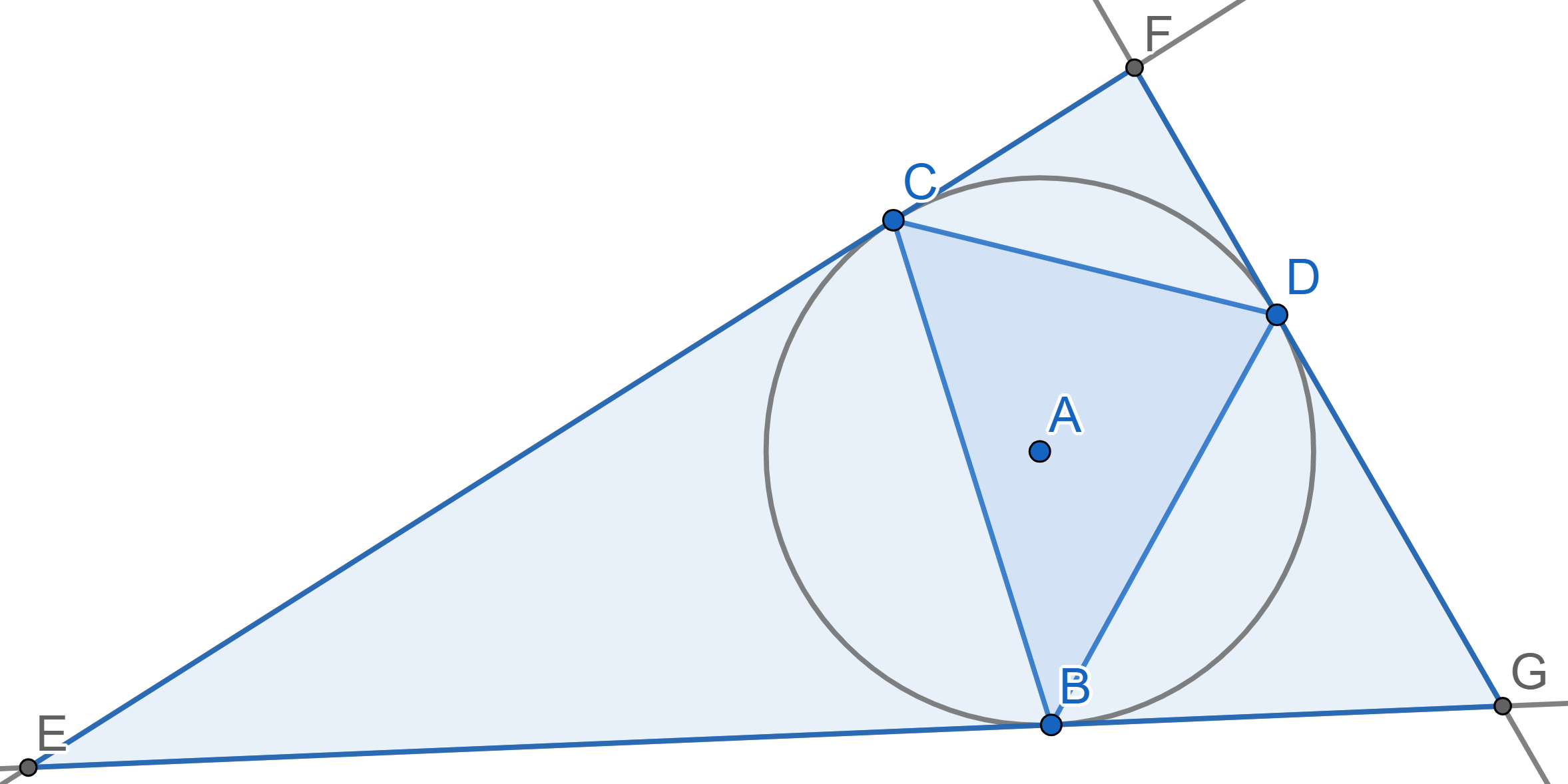
Consider the triangle \(BCD\), inscribed in a circle with center \(A\). The segments \(EF\), \(FG\) and \(EG\) are tangent to the circle at the points \(C\), \(D\) and \(B\) respectively. Prove that the Euler line of the triangle \(BCD\) passes through the center of the circle circumscribed around the triangle \(EFG\).

Show that there are infinitely many integers \(n\) such that \(2^n+1\) is divisible by \(n\). Find all prime numbers that satisfy this property.

If \(k>1\), show that \(k\) does not divide \(2^{k-1}+1\). Find all prime numbers \(p,q\) such that \(2^p+2^q\) is divisible by \(pq\).

Find all pairs \((x,n)\) of positive integers such that \(x^n + 2^n + 1\) is a divisor of \(x^{n+1} + 2^{n+1} + 1\).

Let \(n>1\) be an integer. Show that \(n\) does not divide \(2^n-1\).

Find all integers \(n\) such that \(1^n + 2^n + ... + (n-1)^n\) is divisible by \(n\).

How many integers are there \(n>1\) such that \(a^{25}-a\) is divisible by \(n\) for every integer \(a\).

Let \(p\) be a prime number, \(a\) be an integer, not divisible by \(p\). Prove that \(a^p-a\) is divisible by \(p\).

Let \(n\) be an integer. Denote by \(\phi(n)\) the number of integers from \(1\) to \(n-1\) coprime to \(n\). Find \(\phi(n)\) in the following cases:

• \(n\) is a prime number.

• \(n = p^k\) for a prime \(p\).

• \(n=pq\) for two different primes \(p\) and \(q\).

Let \(n\) be an integer and let \(a\) be an integer coprime to \(n\). Prove that \(a^{\phi(n)-1}-1\) is divisible by \(n\).