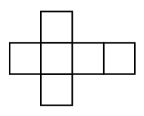
Problems
Take a (finite) set \(S\), say \([n]\) and a random function \(f:S\to S\). What’s the distribution of the limiting size of the image of the iterates of \(f\)?
That is, \(\lim_{N\to\infty}|f^N([n])|\)
By random, let \(i\in[n]\). Each \(f(i)\) is independently and identically distributed as uniform random variables on \([n]\). One can also think of it as \(f\) is taken uniformly from the \(n^n\) possible functions \([n]\to[n]\).
The Great Pyramid of Giza is the largest pyramid in Egypt. For the purposes of this problem, assume that it’s a perfect square-based pyramid, with perpendicular height \(140\)m and the square has side length \(230\)m.
What is its volume in cubic metres?
The volume of a pyramid is \(\frac{1}{3}Bh\), where \(B\) is the area of the base and \(h\) is the perpendicular height. What’s the volume of a regular tetrahedron with side length \(1\)?
A regular octahedron is a solid with eight faces, all of which are equilateral triangles. It can be formed by placing together two square based pyramids at their bases.
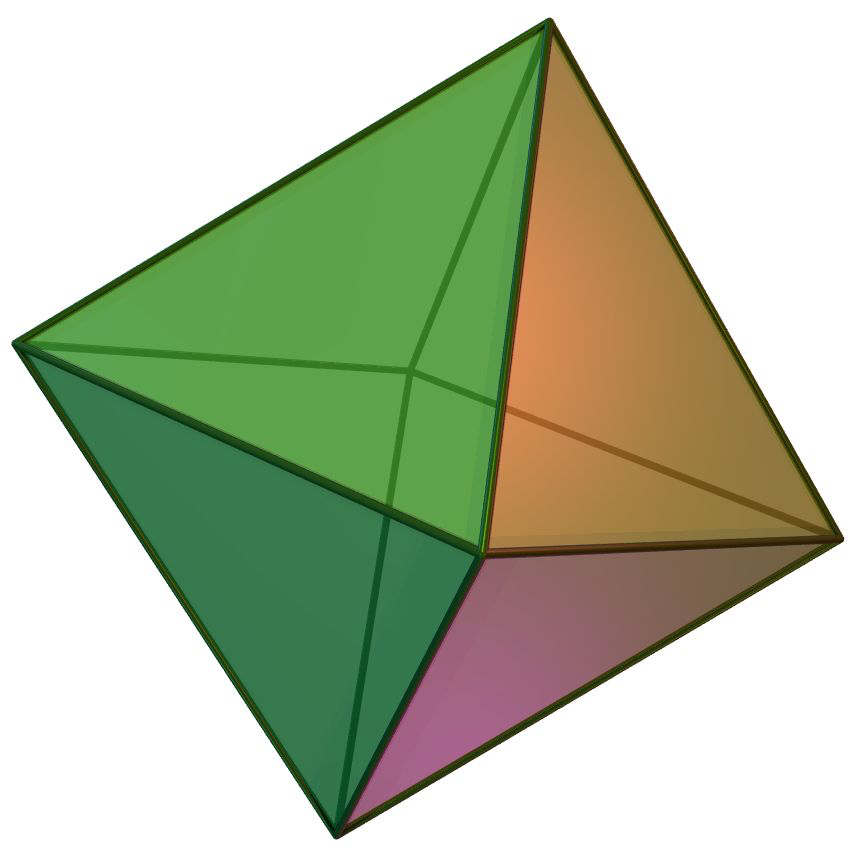
What is the volume of an octahedron with side length \(1\)?
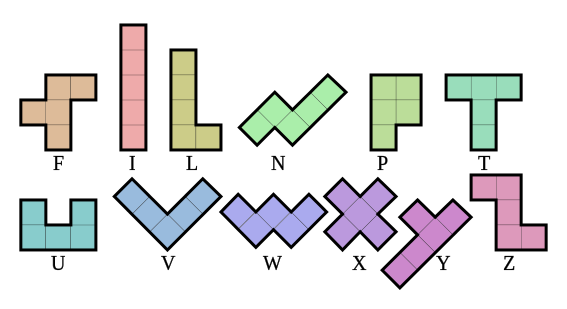
In the picture below, there are the \(12\) pentominoes. Is it possible to tile a \(6\times10\) rectangle with them, using each pentominoe exactly once?
Show how to tile a \(5\times12\) rectangle with the twelve pentominoes.
Show how to tile a \(4\times15\) rectangle with the twelve pentominoes.
Is it possible to tile a \(3\times20\) rectangle with the twelve pentominoes?
How can we tile the plane with this cube net?
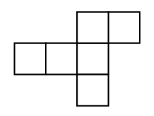
How can we tile the plane with this cube net?