Problems

The director of a bank has forgotten the combination to open the safe! He only remembers the first \(8\) out of \(10\) digits, and that the whole number was divisible by \(45\). Help him out and find all possible pairs of digits which could complete the combination. \[20242025**\]

There are two hourglasses, a small one and a large one. The sand in the small one takes \(7\) minutes to fall all the way through, and the sand in the large one takes \(11\) minutes. How can you measure \(15\) minutes using those?

Two players are playing a game. The first player is thinking of a finite sequence of positive integers \(a_1\), \(a_2\), ..., \(a_n\). The second player can try to find the first player’s sequence by naming their own sequence \(b_1\), \(b_2\), ..., \(b_n\). After this, the first player will give the result \(a_1b_1 + a_2b_2 + ...+a_nb_n\). Then the second player can say another sequence \(c_1\), \(c_2\), ..., \(c_n\) to get another answer \(a_1c_1+ a_2c_2 + ... +a_nc_n\) from the first player. Find the smallest number of sequences the second player has to name to find out the sequence \(a_1\), \(a_2\), ..., \(a_n\).

The letters \(A\), \(R\), \(S\) and \(T\) represent different digits from \(1\) to \(9\). The same letters correspond to the same digits, while different letters correspond to different digits.
Find \(ART\), given that \(ARTS+STAR=10,T31\).

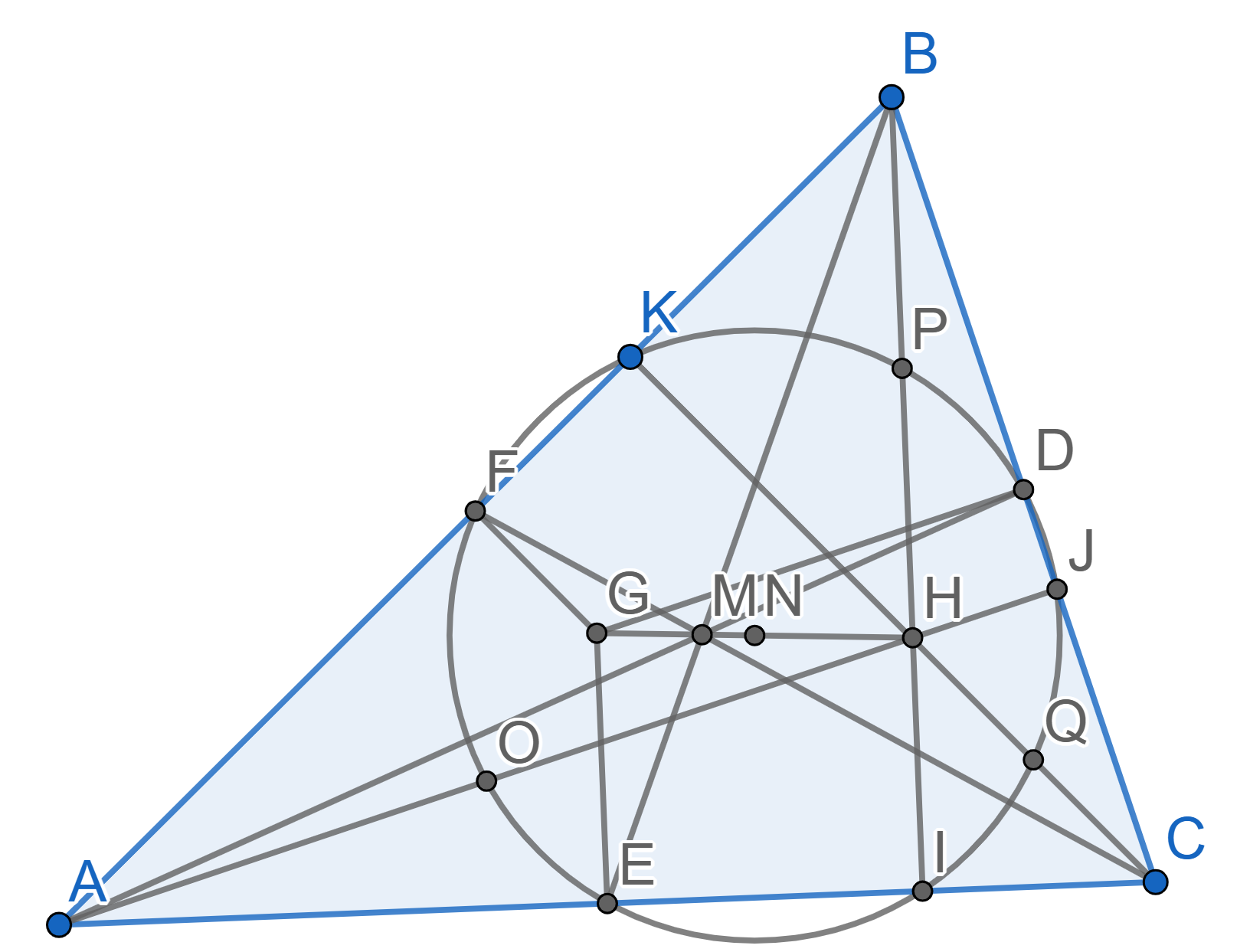
Let \(ABC\) be a non-isosceles triangle. The point \(G\) is the point of intersection of the medians \(AE\), \(BF\), \(CD\). The point \(H\) is the point of intersection of all heights. The point \(I\) is the center of the circumscribed circle of \(ABC\), or the point of intersection of all perpendicular bisectors to the segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one line and that the ratio \(IG:GH = 1:2\). The line that all of \(I\), \(G\) and \(H\) lie on is called the Euler line of triangle \(ABC\).

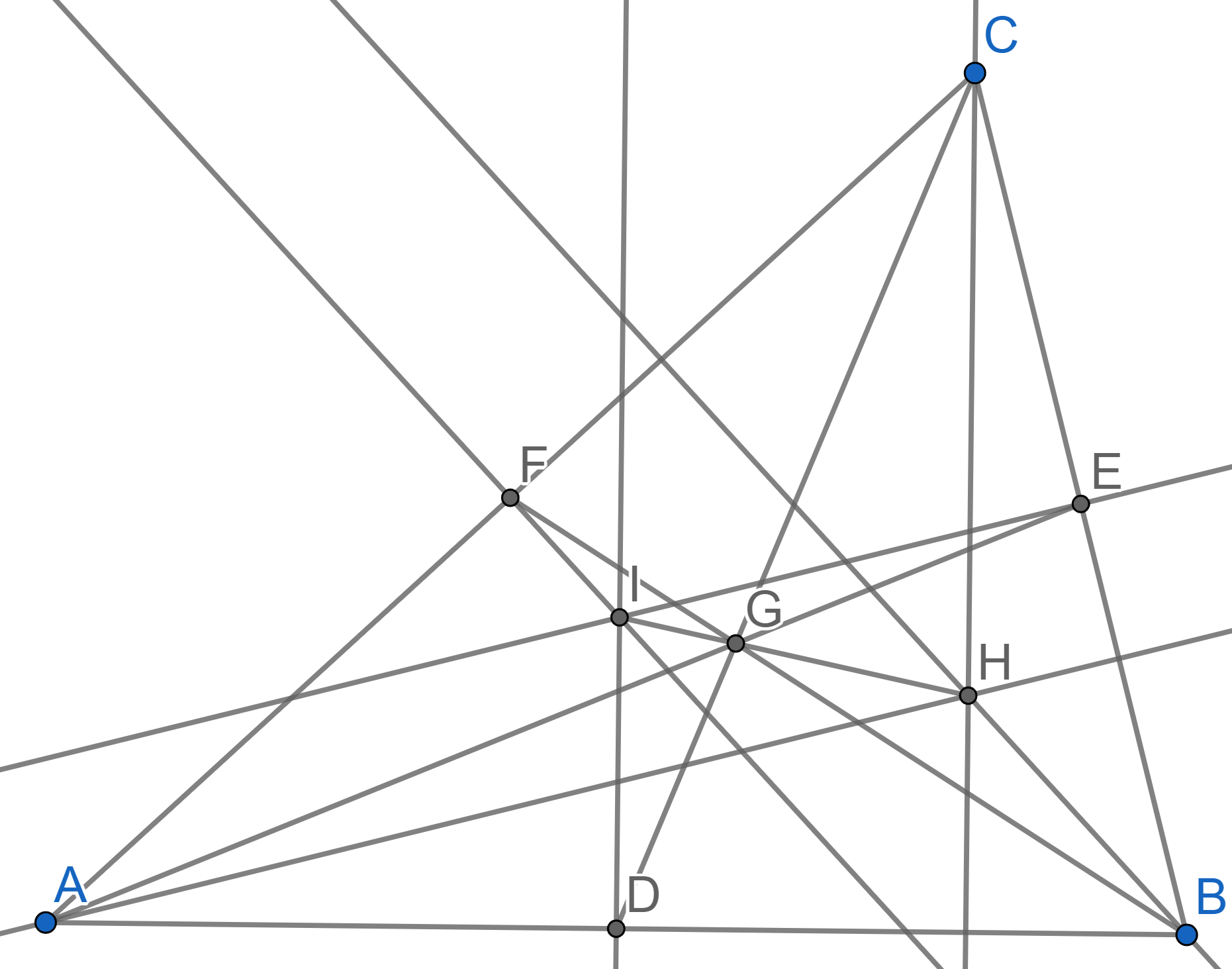
Let \(ABC\) be a triangle. Prove that the heights \(AD\), \(BE\), \(CF\) intersect in one point.

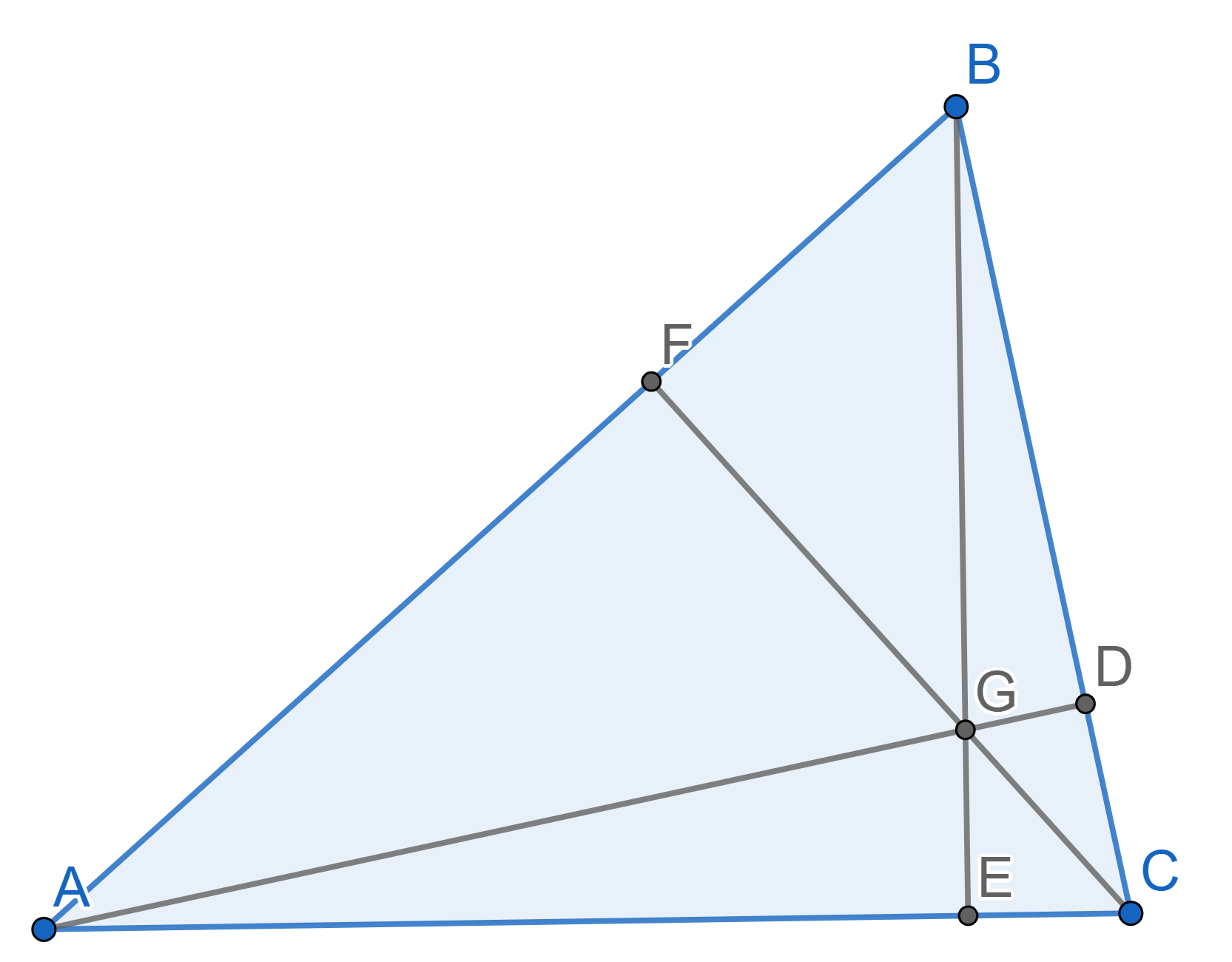
Let \(ABC\) be a triangle. Prove that the medians \(AD\), \(BE\), \(CF\) intersect in one point.

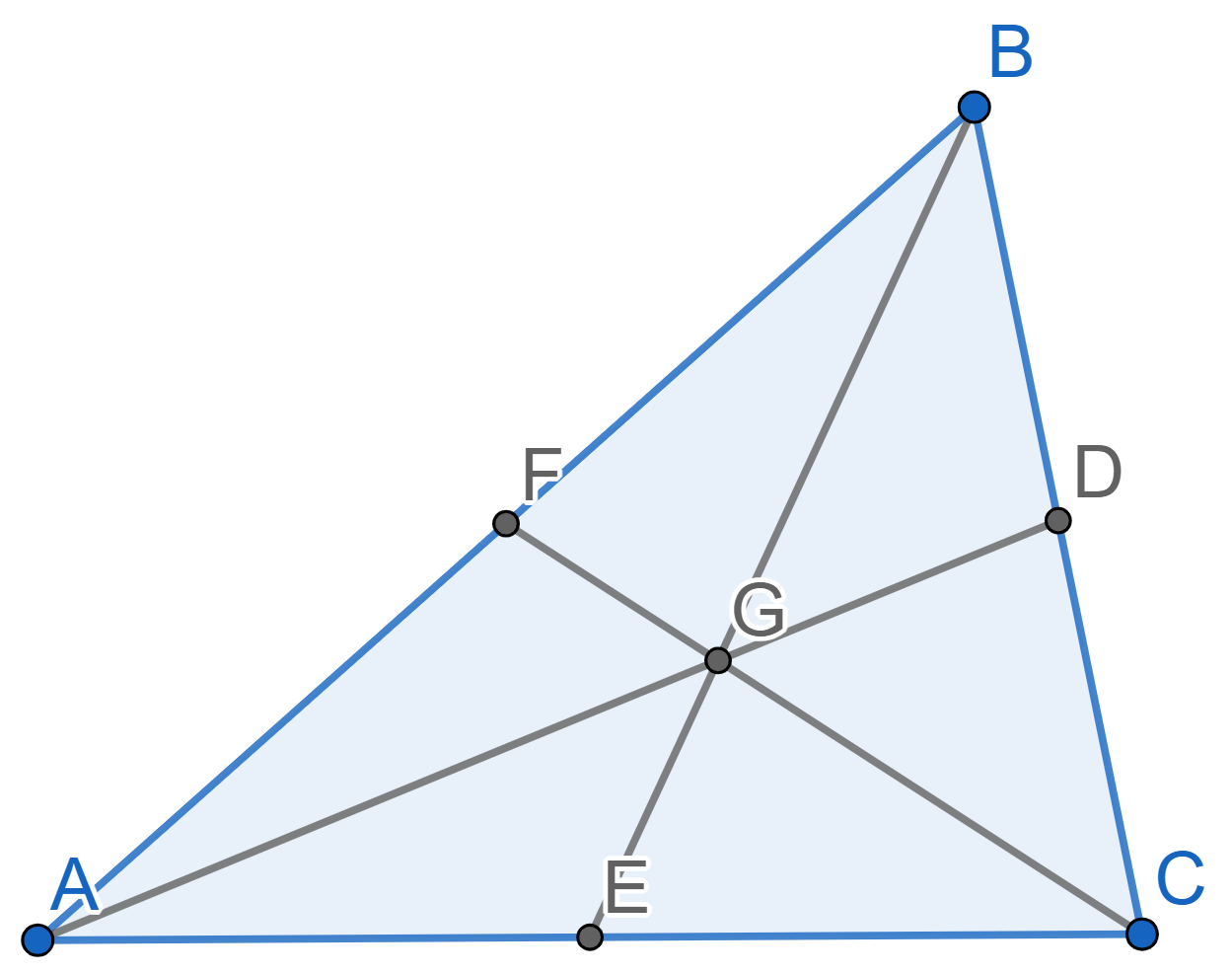
Let \(ABC\) be a triangle with medians \(AD\), \(BE\), \(CF\). Prove that the triangles \(ABC\) and \(DEF\) are similar. What is their similarity coefficient?

Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Prove that the perpendicular bisectors to the sides \(AB\), \(BC\), \(AC\) intersect at one point.

Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\), let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Prove that the points \(D\), \(J\), \(I\), \(E\), \(F\) and \(K\) all lie on one circle.