Problems

One person says: “I’m a liar.” Is he a native of the island of knights and liars?

In a purse, there are 2 coins which make a total of 15 pence. One of them is not a five pence coin. What kind of coins are these?

15 points are placed inside a \(4 \times 4\) square. Prove that it is possible to cut a unit square out of the \(4 \times 4\) square that does not contain any points.

On an island, there are knights who always tell the truth, and liars who always lie. What question would you need to ask the islander to find out if he has a crocodile at home?

What is there a greater number of: cats, except for those cats that are not named Fluffy, or animals named Fluffy, except for those that are not cats?

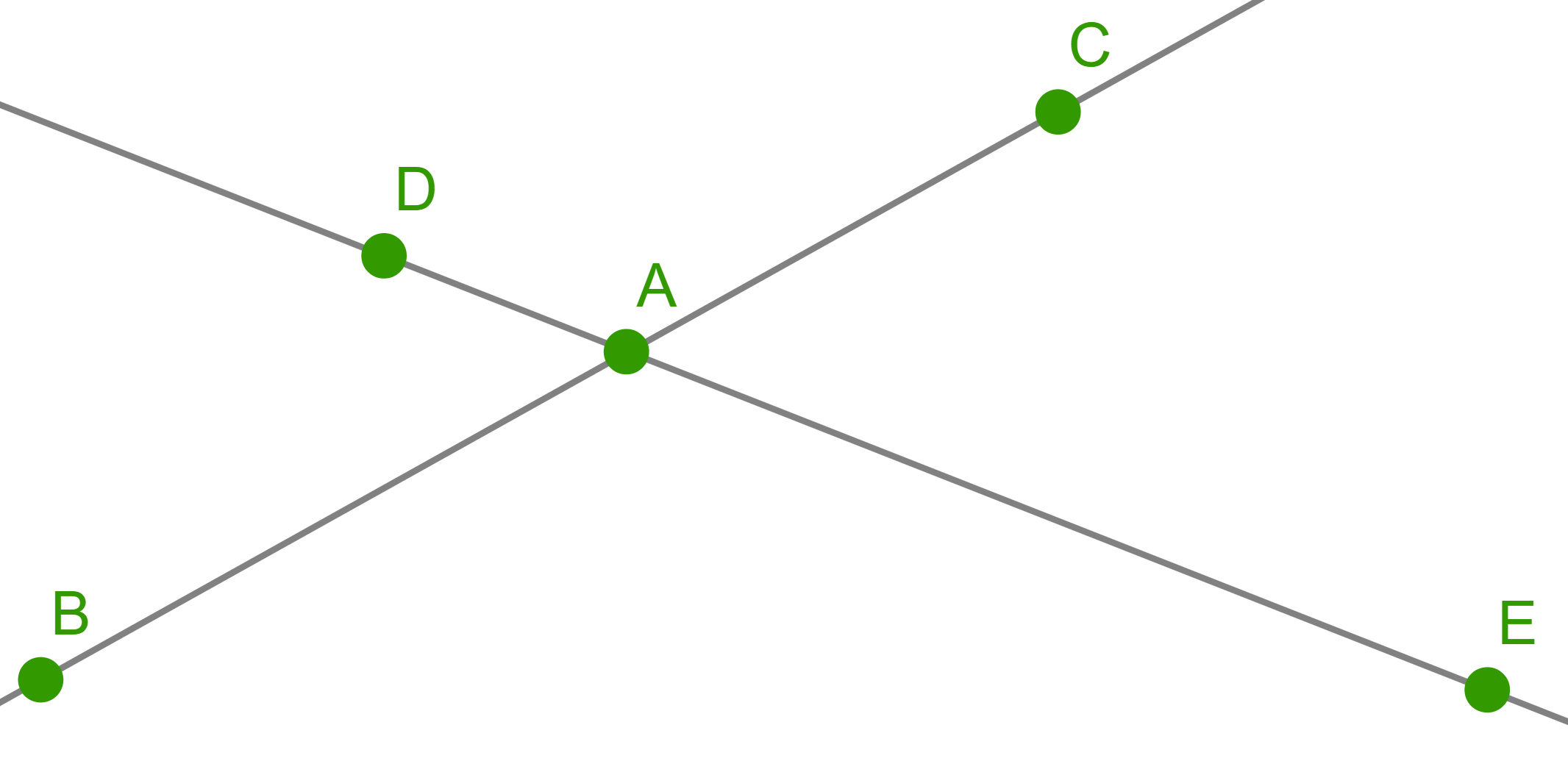
Five oaks are planted along two linear park alleys in such a way that there are three oaks along each alley, see picture. Where should we plant the sixth oak so that it will be possible to lay two more linear alleys, along each of which there would also be three oak trees growing?

The smell of a flowering lavender plant diffuses through a radius of 20 m around it. How many lavender plants must be planted along a straight 400m path so that the smell of the lavender reaches every point on the path.

The angle at the top of a crane is \(20^{\circ}\). How will the magnitude of this angle change when looking at the crane with binoculars which triple the size of everything?

What is the minimum number of squares that need to be marked on a chessboard, so that:

1) There are no horizontally, vertically, or diagonally adjacent marked squares.

2) Adding any single new marked square breaks rule 1.

We are given 101 rectangles with integer-length sides that do not exceed 100.

Prove that amongst them there will be three rectangles \(A, B, C\), which will fit completely inside one another so that \(A \subset B \subset C\).