Problems
16 teams took part in a handball tournament where a victory was worth 2 points, a draw – 1 point and a defeat – 0 points. All teams scored a different number of points, and the team that ranked seventh, scored 21 points. Prove that the winning team drew at least once.
To a certain number, we add the sum of its digits and the answer we get is 2014. Give an example of such a number.
It is known that \(AA + A = XYZ\). What is the last digit of the product: \(B \times C \times D \times D \times C \times E \times F \times G\) (where different letters denote different digits, identical letters denote identical digits)?
There are 40 identical cords. If you set any cord on fire on one side, it burns, and if you set it alight on the other side, it will not burn. Ahmed arranges the cords in the form of a square (see the figure below, each cord makes up a side of a cell). Then, Helen arranges 12 fuses. Will Ahmed be able to lay out the cords in such a way that Helen will not be able to burn all of them?
The pupils of class 5A had a total of 2015 pencils. One of them lost a box with five pencils, and instead bought a box with 50 pencils. How many pencils do the pupils of class 5A now have?
For the anniversary of the London Mathematical Olympiad, the mint coined three commemorative coins. One coin turned out correctly, the second coin on both sides had two heads, and the third had tails on both sides. The director of the mint, without looking, chose one of these three coins and tossed it at random. She got heads. What is the probability that the second side of this coin also has heads?
In one box, there are two pies with mushrooms, in another box there are two with cherries and in the third one, there is one with mushrooms and one with cherries. The pies look and weigh the same, so it’s not known what is in each one. The grandson needs to take one pie to school. The grandmother wants to give him a pie with cherries, but she is confused herself and can only determine the filling by breaking the pie, but the grandson does not want a broken pie, he wants a whole one.
a) Show that the grandmother can act so that the probability of giving the grandson a whole pie with cherries will be equal to \(2/3\).
b) Is there a strategy in which the probability of giving the grandson a whole pie with cherries is higher than \(2/3\)?
In each cell of a board of size \(5\times5\) a cross or a nought is placed, and no three crosses are positioned in a row, either horizontally, vertically or diagonally. What is the largest number of crosses on the board?
An after school club is attended by 4 boys from class 7A, and four from class 7B. Of those who attended three were named Ben, three were named Will, and two were named Tom.
Is it possible for it to be the case that each boy had at least one namesake classmate who attended the club?
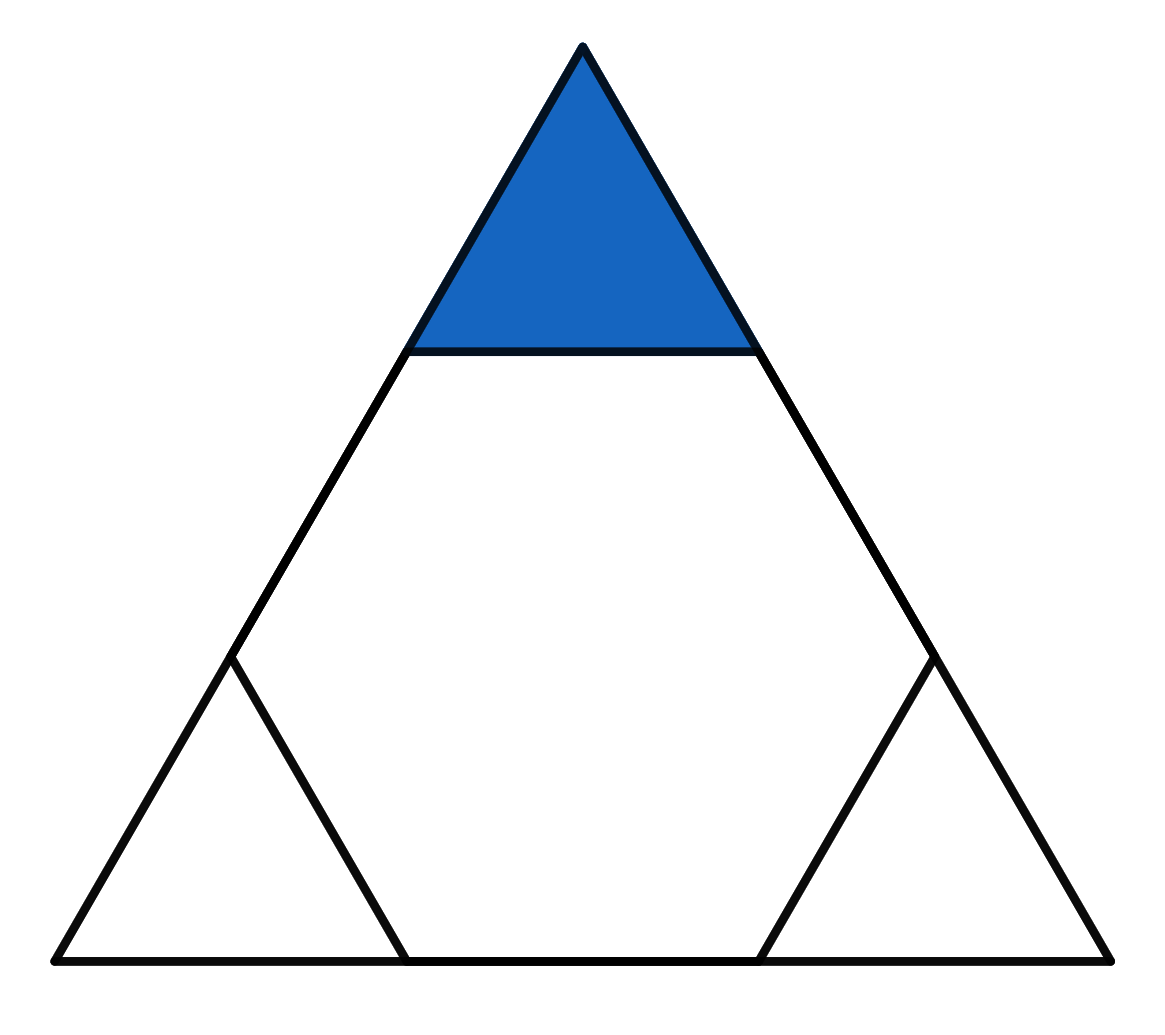
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.