Problems

On the plane coordinate axes with the same but not stated scale and the graph of the function \(y = \sin x\), \(x\) \((0; \alpha)\) are given.

How can you construct a tangent to this graph at a given point using a compass and a ruler if: a) \(\alpha \in (\pi /2; \pi)\); b) \(\alpha \in (0; \pi /2)\)?

The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.

Prove that if the expression

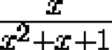
takes a rational value, then the expression

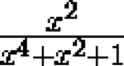
also takes on a rational value.

Which numbers can stand in place of the letters in the equality \(AB \times C = DE\), if different letters denote different numbers and from left to right the numbers are written in ascending order?

There are 40 weights of weights of 1 g, 2 g, ..., 40 grams. Of these, 10 weights of even weight were chosen and placed on the left hand side of the scales. Then we selected 10 weights of odd weight and put it on the right hand side of the scales. The scales were balanced. Prove that on one of the bowls of the scales there are two weights with a mass difference of 20 g.

Mark has 1000 identical cubes, each of which has one pair of opposite faces which are coloured white, another pair which are blue and a third pair that are red. He made a large \(10 \times 10 \times 10\) cube from them, joining cubes to one another which have the same coloured faces. Prove that the large cube has a face which is solidly one colour.

Four numbers (from 1 to 9) have been used to create two numbers with four-digits each. These two numbers are the maximum and minimum numbers, respectively, possible. The sum of these two numbers is equal to 11990. What could the two numbers be?

There are 100 boxes numbered from 1 to 100. In one box there is a prize and the presenter knows where the prize is. The spectator can send the presented a pack of notes with questions that require a “yes” or “no” answer. The presenter mixes the notes in a bag and, without reading out the questions aloud, honestly answers all of them. What is the smallest number of notes you need to send to know for sure where the prize is?

The nonzero numbers \(a\), \(b\), \(c\) are such that every two of the three equations \(ax^{11} + bx^4 + c = 0\), \(bx^{11} + cx^4 + a = 0\), \(cx^{11} + ax^4 + b = 0\) have a common root. Prove that all three equations have a common root.

At a round table, 30 people are sitting – knights and liars (knights always tell the truth, and liars always lie). It is known that each of them at that table has exactly one friend, and for each knight this friend is a liar, and for a liar this friend is a knight (friendship is always mutual). To the question “Does your friend sit next to you?” those in every other seat answered “yes”. How many of the others could also have said “Yes”?