Problems
Using the area of a rectangle prove that \(a\times b=b\times a\).
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a square, or slightly harder in a shape of a given rectangle.
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a hexagon
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a shape like this
Generally, when a line intersects a circle, it creates two different
points of intersection. However, sometimes there is only one point. In
such case we say the line is tangent to the circle. For
example on the picture below the line \(CD\) intersects the circle at two points
\(D\) and \(E\) and the line \(CB\) is tangent to the circle. To solve the
problems today we will need the following theorem.
Theorem: The radius \(AB\) is perpendicular to the tangent line
\(BC\).
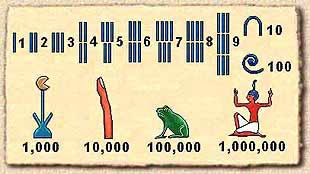
Sometimes one can guess certain multiples of a number just by looking at it, the idea of this sheet is to learn to recognise quickly using tricks when a natural number is divisible by another number.
Sometimes a problem describes a certain process and asks you whether a certain result can be achieved through a series of repeated actions. How could we prove that such a result is impossible to obtain? One of the ways is to observe all the properties of the process that do not change after performing some action, or alternatively, properties that change in a predictable way. We call these properties "Invariants".
Today we will study the method of finding the amount of combinations, or consecutive actions, or ways to select items from a bag which is called the Product rule. The main idea of this combinatorial is the following: if you are asked to perform an action that can be done in, say \(5\) ways and another action afterwards that can be done in \(4\) ways, then the total number of possibilities to perform two consecutive actions would be equal to \(5\times 4\). The reason for this is the opportunity to choose \(4\) possible second actions for each of the \(5\) choices of the first action already made before.
Geometry reminder
We call two polygons congruent if all their corresponding sides and angles are equal. Triangles are the easiest sort of polygons to deal with. Assume we are given two triangles \(ABC\) and \(A_1B_1C_1\) and we need to check whether they are congruent or not, some rules that help are:
If all three corresponding sides of the triangles are equal, then the triangles are congruent.
If, in the given triangles \(ABC\) and \(A_1B_1C_1\), two corresponding sides \(AB=A_1B_1\), \(AC=A_1C_1\) and the angles between them \(\angle BAC = \angle B_1A_1C_1\) are equal, then the triangles are congruent.
If the sides \(AB=A_1B_1\) and pairs of the corresponding angles next to them \(\angle CAB = \angle C_1A_1B_1\) and \(\angle CBA = \angle C_1B_1A_1\) are equal, then the triangles are congruent.
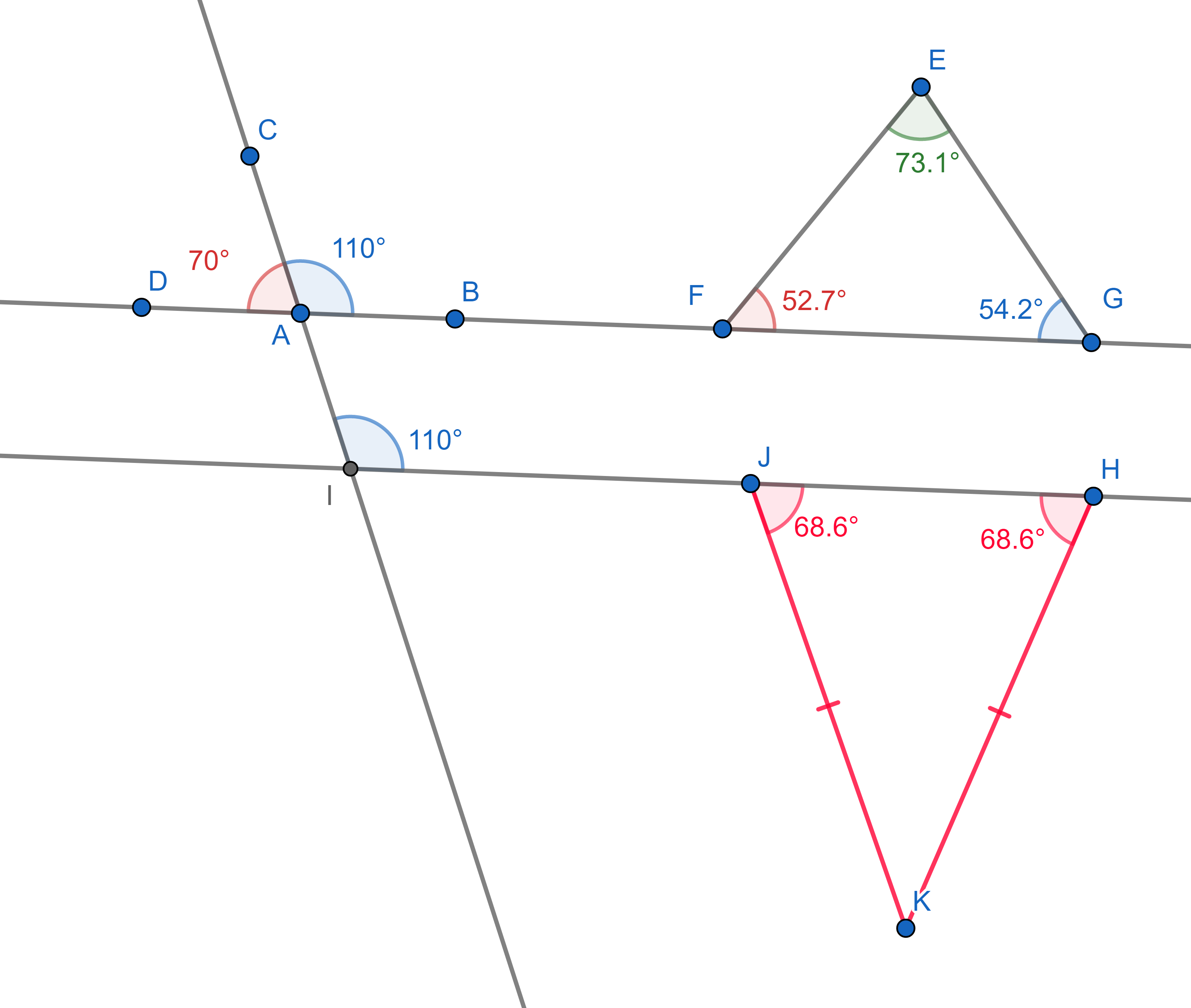
The basic principles about parallel lines and general triangles
are:
1. The supplementary angles (angles "hugging" a straight line) add up to
\(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
3. A line cutting two parallel lines cuts them at the same angles (these
are called corresponding angles).
4. In an isosceles triangle (which has two sides of equal lengths), two
angles touching the third side are equal.