Problems

Cut a square into five triangles in such a way that the area of one of these triangles is equal to the sum of the area of other four triangles.

A circular triangle is a triangle in which the sides are arcs of circles. Below is a circular triangle in which the sides are arcs of circles centered at the vertices opposite to the sides.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of the circular triangle.

In a box there are \(20\) cards of different colours: some red, some blue and some yellow. Yellow cards outnumber red ones and there are six times as many yellow cards as blue cards. We draw some cards from the box without looking. What is the minimum number we need to draw to guarantee a red card among them?

There are two piles of rocks, \(10\) rocks in each pile. Fred and George play a game, taking the rocks away. They are allowed to take any number of rocks only from one pile per turn. The one who has nothing to take loses. If Fred starts, who has the winning strategy?

Theorem: If we mark \(n\) points on a circle and connect each point to every other point by a straight line, the lines divide the interior of the circle is into is \(2n-1\) regions.
"Proof": First, let’s have a look at the smallest natural numbers.

• When \(n=1\) there is one region (the whole disc).

• When \(n=2\) there are two regions (two half-discs).

• When \(n=3\) there are \(4\) regions (three lune-like regions and one triangle in the middle).

• When \(n=4\) there are \(8\) regions, and if you’re still not convinced then try \(n=5\) and you’ll find \(16\) regions if you count carefully.

Our proof in general will be by induction on \(n\). Assuming the theorem is true for \(n\) points, consider a circle with \(n+1\) points on it. Connecting \(n\) of them together in pairs produces \(2n-1\) regions in the disc, and then connecting the remaining point to all the others will divide the previous regions into two parts, thereby giving us \(2\times (2n-1)=2n\) regions.

Let’s "prove" that the number \(1\) is a multiple of \(3\). We will use the symbol \(\equiv\) to denote "congruent modulo \(3\)". Thus, what we need to prove is that \(1\equiv 0\) modulo \(3\). Let’s see: \(1\equiv 4\) modulo \(3\) means that \(2^1\equiv 2^4\) modulo \(3\), thus \(2\equiv 16\) modulo \(3\), however \(16\) gives the remainder \(1\) after division by \(3\), thus we get \(2\equiv 1\) modulo \(3\), next \(2-1\equiv 1-1\) modulo \(3\), and thus \(1\equiv 0\) modulo \(3\). Which means that \(1\) is divisible by \(3\).

Recall that \((n+1)^2=n^2+2n+1\) and after expansion we get \((n+1)^2-(2n+1)=n^2\). Subtract \(n(2n+1)\) from both sides \((n+1)^2-(2n+1)-n(2n+1)=n^2-n(2n+1)\) and rewrite it as \((n+1)^2-(n+1)(2n+1)=n^2-n(2n+1)\).
Now we add \(\frac{(2n+1)^2}{4}\) to both sides: \((n+1)^2-(n+1)(2n+1)+\frac{(2n+1)^2}{4}=n^2-n(2n+1)+\frac{(2n+1)^2}{4}\).
Factor both sides into square: \(((n+1)-\frac{2n+1}{2})^2=(n-\frac{2n+1}{2})^2\).
Now take the square root: \((n+1)-\frac{2n+1}{2}=n-\frac{2n+1}{2}\).
Add \(\frac{2n+1}{2}\) to both sides and we get \(n+1=n\) which is equivalent to \(1=0\).

Look at the following diagram, depicting how to get an extra cell by reshaping triangle.

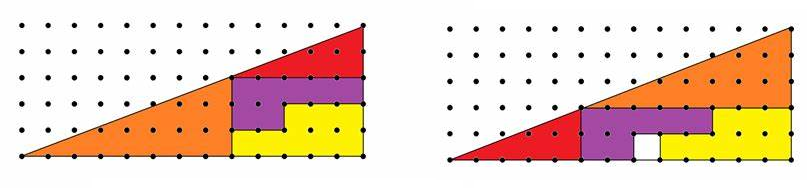
Can you find a mistake? Certainly the triangles have different area, so we cannot obtain one from the other one by reshaping.

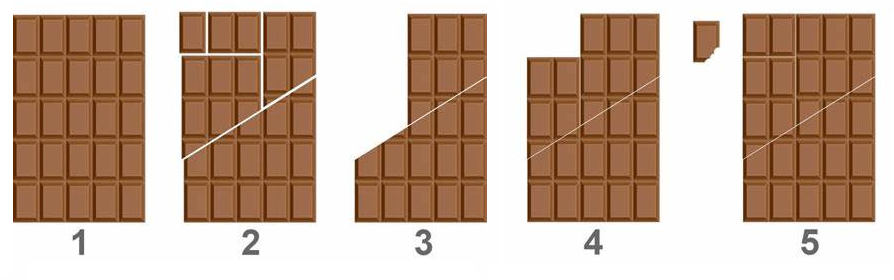
This problem is often called "The infinite chocolate bar". Depicted below is a way to get one more piece of chocolate from the \(5\times 6\) chocolate bar. Do you see where is it wrong?

Consider the following "proof" that any triangle is equilateral: Given a triangle \(ABC\), we first prove that \(AB = AC\). First let’s draw the bisector of the angle \(\angle A\). Now draw the perpendicular bisector of segment \(BC\), denote by \(D\) the middle of \(BC\) and by \(O\) the intersection of these lines. See the diagram

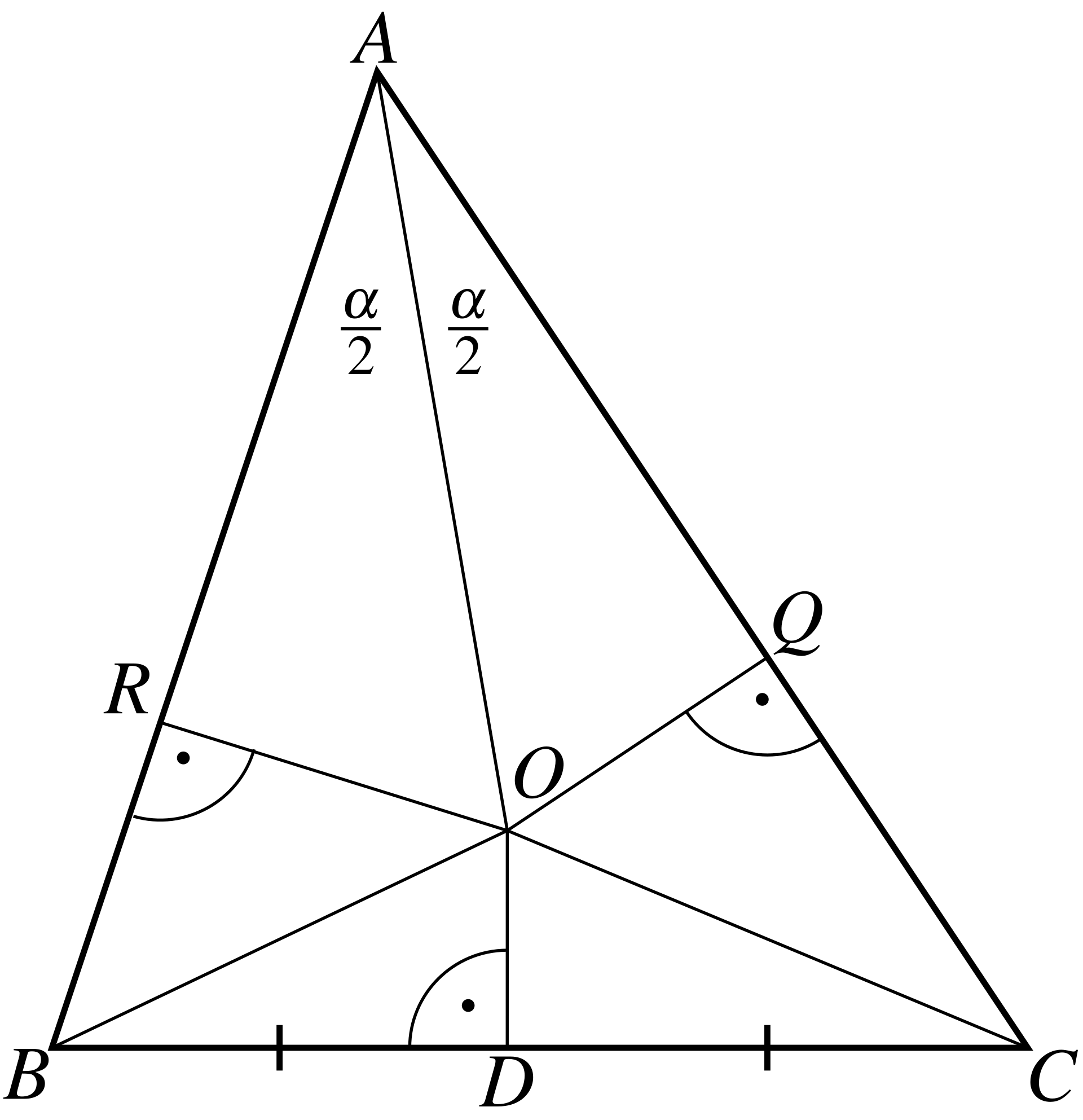
Draw the lines \(OR\) perpendicular to \(AB\) and \(OQ\) perpendicular to \(AC\). Draw lines \(OB\) and \(OC\). Then the triangles, \(RAO\) and \(QAO\) are equal, since we have equal angles \(\angle ORA = \angle OQA = 90°,\) and \(\angle RAO = \angle QAO,\) and the common side \(AO\). On the other hand the triangles \(ROB\) and \(QOC\) are also equal since the angles \(\angle BRO = \angle CQO = 90°\), the hypotenuses \(BO = OC\) the legs \(RO = OQ\). Thus, \(AR = AQ,\) \(RB = QC,\) and \(AB = AR + RB = AQ + QC = AC.\) Q.E.D.

As a corollary, one can show that all the triangles are equilateral, by showing that \(AB = BC\) in the same way.